2012年春晚歌舞类节目成为春晚顶梁柱,尤其是不少创意组合都被网友称赞很有新意.王力宏和李云迪的钢琴PK,加上背景板的黑白键盘,更被网友称赞是行云流水的感觉.某网站从2012年1月23号到1月30做了持续一周的在线调查,共有n人参加调查,现将数据整理分组如题中表格所示.
序号
|
年龄分组
|
组中值
|
频数(人数)
|
频率(f)
|
1
|
[20,25)
|
22.5
|
x
|
s
|
2
|
[25,30)
|
27.5
|
800
|
t
|
3
|
[30,35)
|
32.5
|
y
|
0.40
|
4
|
[35,40)
|
37.5
|
1600
|
0.32
|
5
|
[40,45)
|
42.5
|
z
|
0.04
|
(1)求n及表中x,y,z,s,t的值
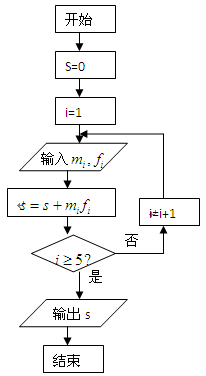
(2)为了对数据进行分析,采用了计算机辅助计算,分析其中一部分计算,见算法流程图,求输出的S值,并说
明S的统计意义.
(3)从年龄在[20,30)岁人群中采用分层抽样法抽取6人参加元宵晚会活动,其中选取2人作为代表发言,求选取2名代表中恰有1人年龄在[25,30)岁的概率.