(本小题共13分)某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
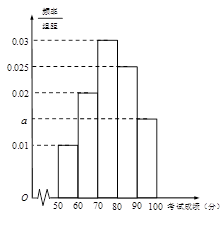
(Ⅰ)求频率分布直方图中的a值;从该市随机选取一名学生,试估计这名学生参加考试的成绩低于90分的概率;
(Ⅱ)设A,B,C三名学生的考试成绩在区间[80,90)内,M,N两名学生的考试成绩在区间[60,70)内,现从这5名学生中任选两人参加座谈会,求学生M,N至少有一人被选中的概率;
(Ⅲ)试估计样本的中位数落在哪个分组区间内 (只需写出结论).
(注:将频率视为相应的概率)