已知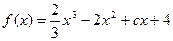
，
，
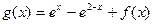（1）若f(x)在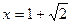
处取得极值，试求c的值和f(x)的单调增区间；
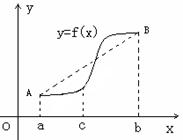
（2）如右图所示，若函数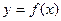
的图象在
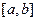连续光滑，试猜想拉格朗日中值定理：即一定存在
使得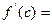
？（用含有a,b,f(a),f(b)的表达式直接回答）
（3）利用（2）证明：函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
，
，且
，求
值．
（
为常数）的值域．
，
，且
，
，求
．
的奇偶性．
，求下列各式的值．
；（２）
．推荐套卷
已知，，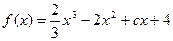
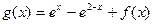（1）若f(x)在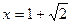处取得极值，试求c的值和f(x)的单调增区间；
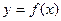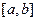（2）如右图所示，若函数的图象在连续光滑，试猜想拉格朗日中值定理：即一定存在使得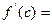？（用含有a,b,f(a),f(b)的表达式直接回答）
（3）利用（2）证明：函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
粤公网安备 44130202000953号