设曲线Ｃ：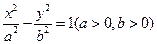
的离心率为
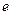，右准线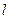
与两渐近线交于Ｐ，Ｑ两点，其右焦点为Ｆ，且△PQF为等边三角形。
（1）求双曲线C的离心率；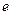
（2）若双曲线C被直线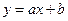
截得弦长为
，求双曲线方程；
（3）设双曲线C经过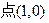
，以F为左焦点，为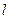左准线的椭圆的短轴端点为B，求BF 中点的轨迹N方程。
相关试题
．
的单调区间；
中，角
的对边分别为
，若
，求
关于直线
的对称点仍在圆上，且与直线
相交的弦长为
，求圆的方程．
．
，求m的值．
中，
=
，
=1，
与平面
所成角的大小；
与平面
所成二面角的正弦值
是正常数，
，
，求证：
，指出等号成立的条件；
（
）的最小值，指出取最小值时
的值．推荐套卷
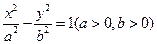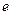设曲线Ｃ：的离心率为，右准线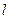与两渐近线交于Ｐ，Ｑ两点，其右焦点为Ｆ，且△PQF为等边三角形。
（1）求双曲线C的离心率；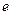
（2）若双曲线C被直线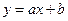截得弦长为，求双曲线方程；
（3）设双曲线C经过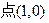，以F为左焦点，为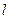左准线的椭圆的短轴端点为B，求BF 中点的轨迹N方程。
粤公网安备 44130202000953号