如图，平面直角坐标系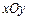
中，
和
为两等腰直角三角形，
，C(a,0)(a>0)．设和的外接圆圆心分别为
,
．
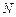（Ⅰ）若⊙M与直线CD相切，求直线CD的方程；
（Ⅱ）若直线AB截⊙N所得弦长为4，求⊙N的标准方程；
（Ⅲ）是否存在这样的⊙N，使得⊙N上有且只有三个点到直线AB的距离为
，若存在，求此时⊙N的标准方程；若不存在，说明理由．
相关试题
和400π
，其中
时，判断函数
在定义域上的单调性；
，不等式
都成立。
的前n项和为
，且
。
是等比数列；
满足
，且
，求数列
。
的最小正周期及在区间
上的最大值和最小值；
，
，求
的值。
，
，其中
，a、b为常数，已知曲线
在点（2,0）处有相同的切线
。
单调区间与极值。推荐套卷
如图，平面直角坐标系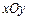中，和为两等腰直角三角形，，C(a,0)(a>0)．设和的外接圆圆心分别为,．
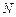（Ⅰ）若⊙M与直线CD相切，求直线CD的方程；
（Ⅱ）若直线AB截⊙N所得弦长为4，求⊙N的标准方程；
（Ⅲ）是否存在这样的⊙N，使得⊙N上有且只有三个点到直线AB的距离为，若存在，求此时⊙N的标准方程；若不存在，说明理由．
粤公网安备 44130202000953号