已知函数f（x）=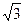
sin
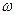xcos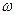x－cos2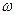x，其中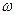为使函数f（x）能在x=
时取得最大值时的最小正整数．
（1）求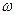的值；
（2）设△ABC的三边
a、b、c满足b2=ac，且边b所对的角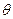
的取值集合为A，当x
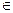A时，求函数f（x）的值域．
相关试题
的奇偶性。 (2)判断函数
的定义域：
，当
时f(x)>0，
时f(x)<0
的解集为R.
t + 30 (1 ≤ t ≤ 30 , t ∈ N )，后20天价格为g (t) =" 45" (31 ≤ t ≤ 50 , t ∈ N )．相关知识点
推荐套卷
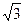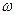已知函数f（x）=sinxcos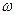x－cos2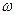x，其中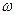为使函数f（x）能在x= 时取得最大值时的最小正整数．
（1）求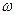的值；
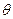（2）设△ABC的三边a、b、c满足b2=ac，且边b所对的角的取值集合为A，当x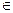A时，求函数f（x）的值域．
粤公网安备 44130202000953号