定义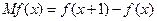
为函数
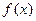的边际函数，某企业每月最多生产
台报警器，已知每生产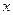
台的收入函数为
（单位：元），其成本函数为
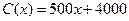（单位：元），利润是收入与成本的差。（1）求利润函数
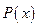及其边际函数
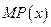；（2）利润函数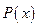及其边际函数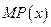是否有相等的最大值？请说明理由。
相关试题
的内角
的对边分别为
，
． 
，
，求
的值；
，求
的值．
的各项均为正整数，对于任意n∈N*，都有
成立，且
．
，
的值；
中，已知
，
，
，点
，
分别在棱
，
上，且
，
，
． 
时，求异面直线
与
所成角的大小；
与平面
所成角的正弦值为
时，求
的值．
的不等式
的解集为R，求实数
的取值范围
中，已知曲线
的参数方程是
（
是参数），若以
为极点，
轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线推荐套卷
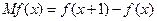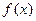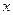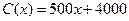定义为函数的边际函数，某企业每月最多生产台报警器，已知每生产台的收入函数为（单位：元），其成本函数为（单位：元），利润是收入与成本的差。（1）求利润函数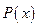及其边际函数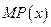；（2）利润函数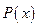及其边际函数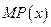是否有相等的最大值？请说明理由。
粤公网安备 44130202000953号