（本小题满分12分）学校餐厅每天供应1000名学生用餐，每星期一有A、B两样特色菜可供选择（每个学生都将从二者中选一），调查资料表明，凡是在本周星期一选A菜的，下周星期一会有20％改选B，而选B菜的，下周星期一则有30％改选A，若用A
、B分别表示在第n个星期一选A、B菜的人数。（1）试以A表示A
；（2）若A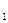
=200，求{A}的通项公式；（3）问第n个星期一时，选A与选B的人数相等？
相关试题
，
，
，求
；
，求实数
的取值范围。
的顶点在原点，始边与
轴的非负半轴重合，终边经过点
，
的值。
，求
的值。
是定义域在
上的不恒为零的函数，且对于任意非零实数
满足
.
与
的值；
的奇偶性；
上单调递减，求不等式
的解集.
在定义域
上是增函数且为奇函数，且
，求实数
的取值范围.
，求
的取值范围.推荐套卷
（本小题满分12分）学校餐厅每天供应1000名学生用餐，每星期一有A、B两样特色菜可供选择（每个学生都将从二者中选一），调查资料表明，凡是在本周星期一选A菜的，下周星期一会有20％改选B，而选B菜的，下周星期一则有30％改选A，若用A、B分别表示在第n个星期一选A、B菜的人数。（1）试以A表示A；（2）若A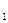=200，求{A}的通项公式；（3）问第n个星期一时，选A与选B的人数相等？
粤公网安备 44130202000953号