（本小题满分12分）如图，斜三棱柱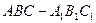
，已知侧面
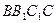与底面ABC垂直且∠BCA =90°，∠
，
=2，若二面角
为30°. （Ⅰ）证明
； 
（Ⅱ）求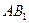
与平面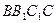所成角的正切值；
（Ⅲ）在平面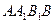
内找一点P，使三棱锥
为正三棱锥，并求P到平面
距离.
，
，且
，求
，
的值
，
，若
，求
的取值范围．
，
，
，
，
，求：
的
值；
，
的
的
，
，且
，求
，
的值
，
，
，求
的值．推荐套卷
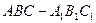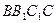（本小题满分12分）如图，斜三棱柱，已知侧面与底面ABC垂直且∠BCA =90°，∠，=2，若二面角为30°. （Ⅰ）证明；
（Ⅱ）求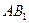与平面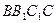所成角的正切值；
（Ⅲ）在平面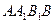内找一点P，使三棱锥为正三棱锥，并求P到平面距离.
粤公网安备 44130202000953号