(本小题满分13分)某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.(Ⅰ)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;(Ⅱ)现有两个奖励函数模型:(1)y=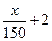 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
推荐套卷
(本小题满分13分)某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.(Ⅰ)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;(Ⅱ)现有两个奖励函数模型:(1)y=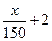 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?