（本小题满分16分）已知集合M是满足下列性质的函数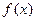
的全体：若存在非零常数k，对任意
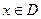，等式
恒成立。（Ⅰ）判断一次函数
是否属于集合M；（Ⅱ）证明
属于集合M，并找到一个常数k；（Ⅲ）已知函数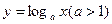
与
的图像有公共点，试证明
为△
内的两点，且
=
+
=
的面积与△
的面积比
对任意的
都有
，设向量
，
，
，
，当
时，求
解集
与圆
:
交于
两点，若圆
的圆心在线段
上，且圆
上，求圆
，
，
满足3
+5
=7，
满足
，若不等式
恒成立，求
最大值推荐套卷
（本小题满分16分）已知集合M是满足下列性质的函数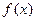的全体：若存在非零常数k，对任意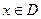，等式恒成立。（Ⅰ）判断一次函数是否属于集合M；（Ⅱ）证明属于集合M，并找到一个常数k；（Ⅲ）已知函数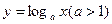与的图像有公共点，试证明
粤公网安备 44130202000953号