由代数式的乘法法则类比推导向量的数量积的运算法则：
①“mn=nm”类比得到“a·b=b·a”；
②“（m+n）t=mt+nt”类比得到“（a+b）·c=a·c+b·c”；
③“t≠ 0，mt=nt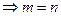
”类比得到“
”；
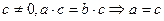④“
”类比得到“
”．
以上类比得到的正确结论的序号是 （写出所有正确结论的序号）．
相关试题
中，若
，则
．
:
，定点
，在
，则
的概率等于 .
，则整数
值为 .
，
，
，
，
的平均数为3，则
的最大值为 .
，且
，则
＿＿＿相关知识点
推荐套卷
由代数式的乘法法则类比推导向量的数量积的运算法则：
①“mn=nm”类比得到“a·b=b·a”；
②“（m+n）t=mt+nt”类比得到“（a+b）·c=a·c+b·c”；
③“t≠ 0，mt=nt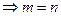”类比得到“”；
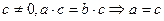④“”类比得到“”．
以上类比得到的正确结论的序号是 （写出所有正确结论的序号）．
粤公网安备 44130202000953号