一个小正方体的六个面，三个面上标以数字0，两个面上标以数学1，一个面上标以数字2
（1）甲、乙两人各抛掷一次，谁的点数大谁就胜，求甲获胜的概率
（2）将这个小正方体抛掷两次，用随机变量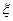
表示向上点数之积，求随机变量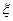的概率分布列及数学期望
相关试题
．
在
上的值域；
，不等式
恒成立，求
．
，
，
,
．
；
，求
的取值范围．
中，内角
的对边分别为
且
．
的值；
，求
．
且
．证明：
；
．
：
（
为参数），
：
（
为参数）．
对应的参数为
，
为
中点
到直线
（推荐套卷
一个小正方体的六个面，三个面上标以数字0，两个面上标以数学1，一个面上标以数字2
（1）甲、乙两人各抛掷一次，谁的点数大谁就胜，求甲获胜的概率
（2）将这个小正方体抛掷两次，用随机变量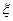表示向上点数之积，求随机变量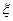的概率分布列及数学期望
粤公网安备 44130202000953号