（本小题满分13分）已知数列{an}，定义
（n∈N+）是数列{an}的倒均数． （1）若数列{an}的倒均数是
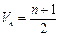，求数列{an}的通项公式；（2）若等比数列{bn}的首项为–1，公比为q =
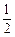，其倒均数为Vn，问是否存在正整数m，使得当n≥m(n∈N+)时，Vn<–16恒成立？若存在，求m的最小值；若不存在，请说明理由．
上一点
，用斜率定义求：
，判断
在
处是否可导？
在点
处可导，则函数
的导数
是可导函数）
；推荐套卷
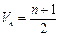（本小题满分13分）已知数列{an}，定义（n∈N+）是数列{an}的倒均数． （1）若数列{an}的倒均数是，求数列{an}的通项公式；（2）若等比数列{bn}的首项为–1，公比为q =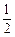，其倒均数为Vn，问是否存在正整数m，使得当n≥m(n∈N+)时，Vn<–16恒成立？若存在，求m的最小值；若不存在，请说明理由．
粤公网安备 44130202000953号