（本小题满分13分）已知椭圆的中心在原点O，短轴长为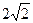
，其焦点F（c，0）（c＞0）对应的准线l与x轴交于A点，|OF|=2|FA|，过A的直线与椭圆交于P、Q两点.
（1）求椭圆的方程；（2）若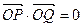
，求直线PQ的方程； （3）设
，过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
相关试题
（1）求边AB的值；（2）求sin(B－C)的值。
中，
，
是
上的一个动点，
最小时，求
的值。
时，求
中,
,
分别是角
所对的边.
； (Ⅱ)若
,
,求推荐套卷
（本小题满分13分）已知椭圆的中心在原点O，短轴长为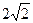，其焦点F（c，0）（c＞0）对应的准线l与x轴交于A点，|OF|=2|FA|，过A的直线与椭圆交于P、Q两点.
（1）求椭圆的方程；（2）若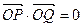，求直线PQ的方程； （3）设，过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
粤公网安备 44130202000953号