(本小题满分13分)用一块长为a,宽为b (a>b)的矩形木块,在二面角为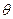 (0<
(0<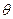 <
<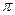 )的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.
)的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.
推荐套卷
(本小题满分13分)用一块长为a,宽为b (a>b)的矩形木块,在二面角为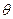 (0<
(0<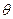 <
<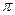 )的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.
)的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.