(理)过点P(1,0)作曲线 的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为
的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为 .
.
(1)求证数列 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)求证: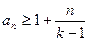 ;(3)当
;(3)当 的前n项和Sn.
的前n项和Sn.
推荐套卷
(理)过点P(1,0)作曲线 的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为
的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为 .
.
(1)求证数列 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)求证: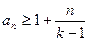 ;(3)当
;(3)当 的前n项和Sn.
的前n项和Sn.