(本小题满分15分)已知二次函数 满足条件:①
满足条件:①  ; ②
; ②  的最小值为
的最小值为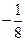 .
.
(1) 求函数 的解析式; (2) 设数列
的解析式; (2) 设数列 的前
的前 项积为
项积为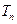 , 且
, 且 , 求数列
, 求数列 的通项公式; (3) 在(2)的条件下, 求数列
的通项公式; (3) 在(2)的条件下, 求数列 的前
的前 项的和.
项的和.
推荐套卷
(本小题满分15分)已知二次函数 满足条件:①
满足条件:①  ; ②
; ②  的最小值为
的最小值为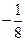 .
.
(1) 求函数 的解析式; (2) 设数列
的解析式; (2) 设数列 的前
的前 项积为
项积为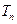 , 且
, 且 , 求数列
, 求数列 的通项公式; (3) 在(2)的条件下, 求数列
的通项公式; (3) 在(2)的条件下, 求数列 的前
的前 项的和.
项的和.