(本小题满分14分)已知椭圆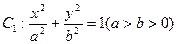 ,它的离心率为
,它的离心率为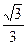 ,直线
,直线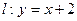 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆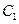 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆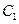 的方程;⑵设椭圆
的方程;⑵设椭圆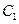 的左焦点为
的左焦点为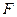 ,左准线为
,左准线为 ,动直线
,动直线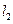 垂直于直线
垂直于直线 ,垂足为点
,垂足为点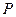 ,线段
,线段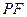 的垂直平分线交
的垂直平分线交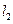 于点
于点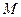 ,求动点
,求动点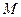 的轨迹
的轨迹 的方程;⑶将曲线
的方程;⑶将曲线 向右平移2个单位得到曲线
向右平移2个单位得到曲线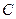 ,设曲线
,设曲线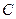 的准线为
的准线为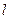 ,焦点为
,焦点为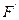 ,过
,过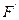 作直线
作直线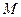 交曲线
交曲线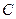 于
于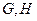 两点,过点
两点,过点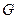 作平行于曲线
作平行于曲线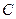 的对称轴的直线
的对称轴的直线 ,若
,若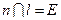 ,试证明三点
,试证明三点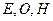 (
(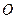 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.
推荐套卷
(本小题满分14分)已知椭圆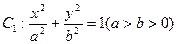 ,它的离心率为
,它的离心率为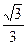 ,直线
,直线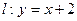 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆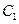 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆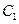 的方程;⑵设椭圆
的方程;⑵设椭圆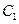 的左焦点为
的左焦点为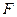 ,左准线为
,左准线为 ,动直线
,动直线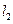 垂直于直线
垂直于直线 ,垂足为点
,垂足为点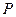 ,线段
,线段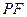 的垂直平分线交
的垂直平分线交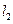 于点
于点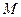 ,求动点
,求动点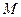 的轨迹
的轨迹 的方程;⑶将曲线
的方程;⑶将曲线 向右平移2个单位得到曲线
向右平移2个单位得到曲线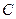 ,设曲线
,设曲线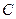 的准线为
的准线为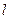 ,焦点为
,焦点为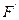 ,过
,过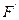 作直线
作直线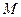 交曲线
交曲线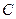 于
于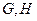 两点,过点
两点,过点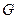 作平行于曲线
作平行于曲线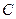 的对称轴的直线
的对称轴的直线 ,若
,若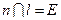 ,试证明三点
,试证明三点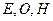 (
(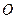 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.