（本小题满分14分）若椭圆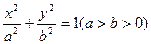
过点
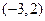，离心率为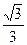
，⊙O的圆心在原点，直径为椭圆的短轴，⊙M的方程为
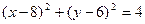，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B. (1) 求椭圆的方程；（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的方程。
相关试题
，曲线y＝f(x)在点(1，f(1))处的切线方程为x＋2y－3＝0.求a，b.推荐套卷
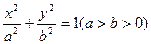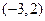（本小题满分14分）若椭圆过点，离心率为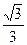，⊙O的圆心在原点，直径为椭圆的短轴，⊙M的方程为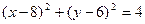，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B. (1) 求椭圆的方程；（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的方程。
粤公网安备 44130202000953号