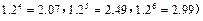某企业为了适应市场需求，计划从2010年元月起，在每月固定投资5万元的基础上，元月份追加投资6万元，以后每月的追加投资额均为之前几个月投资额总和的20%，但每月追加部分最高限额为10万元. 记第n个月的投资额为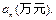
（1）求
与n的关系式；
（2）预计2010年全年共需投资多少万元？（精确到0.01，参考数据：
相关试题
．
的最小正周期和图像的对称轴方程；
上的值域．
．
的单调递增区间；
，
，求
的值．
中，
，
，
分别是三内角A，B，C所对的三边，已知
．
，试判断
，且0＜
＜
＜
．
的值；
（
，
是不同时为零的常数）．
时，若不等式
对任意
恒成立，求实数
在
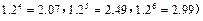
内至少存在一个零点．推荐套卷
某企业为了适应市场需求，计划从2010年元月起，在每月固定投资5万元的基础上，元月份追加投资6万元，以后每月的追加投资额均为之前几个月投资额总和的20%，但每月追加部分最高限额为10万元. 记第n个月的投资额为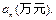
（1）求与n的关系式；
（2）预计2010年全年共需投资多少万元？（精确到0.01，参考数据：
粤公网安备 44130202000953号