河北省唐山市高三年级摸底考试理科数学试卷
已知集合M={x|x≥-1},N={x|2-x2≥0},则M∪N=( )
| A.[-1,+∞) | B.[-1,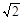 ] ] |
C.[-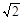 ,+∞) ,+∞) |
D.(-∞,-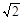 ]∪[-1,+∞) ]∪[-1,+∞) |
复数z=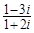 ,则( )
,则( )
| A.|z|=2 | B.z的实部为1 |
| C.z的虚部为-i | D.z的共轭复数为-1+i |
函数f(x)=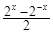 是( )
是( )
| A.偶函数,在(0,+∞)是增函数 |
| B.奇函数,在(0,+∞)是增函数 |
| C.偶函数,在(0,+∞)是减函数 |
| D.奇函数,在(0,+∞)是减函数 |
抛物线y=2ax2(a≠0)的焦点是( )
A.(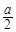 ,0) ,0) |
B.(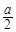 ,0)或(- ,0)或(-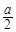 ,0) ,0) |
C.(0, ) ) |
D.(0, )或(0,- )或(0,- ) ) |
高三毕业时,甲、乙、丙、丁四位同学站成一排照相留念,已知甲乙相邻,则甲丙相邻的概率为( )
A.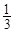 |
B.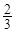 |
C.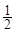 |
D. |
设向量a,b满足|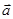 |=|
|=|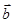 |=|
|=|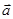 +
+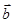 |=1,则|
|=1,则|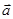 -t
-t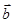 |(t∈R)的最小值为( )
|(t∈R)的最小值为( )
A.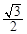 |
B.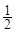 |
C.1 | D.2 |
已知a>0,x,y满足约束条件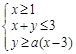 ,且z=2x+y的最小值为1,则a=( )
,且z=2x+y的最小值为1,则a=( )
| A.1 | B.2 | C.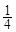 |
D.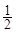 |
将函数f(x)=sinωx(其中ω>0)的图象向右平移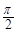 个单位长度,所得图象关于
个单位长度,所得图象关于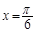 对称,则ω的最小值是( )
对称,则ω的最小值是( )
| A.6 | B.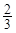 |
C.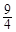 |
D.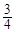 |
已知a>0,且a≠1,则函数f(x)=ax+(x-1)2-2a的零点个数为( )
| A.1 | B.2 | C.3 | D.与a有关 |
某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
| A.5π | B.12π | C.20π | D.8π |

已知双曲线C: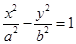 (a>0,b>0)的一条渐近线与直线l:
(a>0,b>0)的一条渐近线与直线l: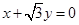 垂直,C的一个焦点到l的距离为1,则C的方程为__________________.
垂直,C的一个焦点到l的距离为1,则C的方程为__________________.
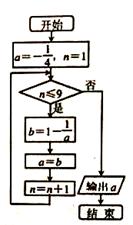
已知等差数列{an}的前n项和为Sn,Sn=kn(n+1)-n(k∈R),公差d为2.
(1)求an与k;
(2)若数列{bn}满足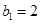 ,
,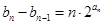 (n≥2),求bn.
(n≥2),求bn.
某大学外语系有5名大学生参加南京青奥会翻译志愿者服务,每名大学生都随机分配到奥体中心体操和游泳两个比赛项目(每名大学生只参加一个项目的服务)。
(1)求5名大学生中恰有2名被分配到体操项目的概率;
(2)设X,Y分别表示5名大学生分配到体操、游泳项目的人数,记ξ=|X-Y|,求随机变量ξ的分布列和数学期望E(ξ).
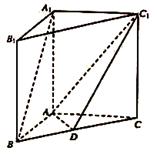
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.
椭圆C: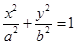 (a>b>0)的离心率为
(a>b>0)的离心率为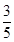 ,P(m,0)为C的长轴上的一个动点,过P点斜率为
,P(m,0)为C的长轴上的一个动点,过P点斜率为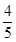 的直线l交C于A、B两点.当m=0时,
的直线l交C于A、B两点.当m=0时,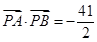
(1)求C的方程;
(2)证明: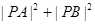 为定值.
为定值.
已知函数f(x)=2ex-ax-2(a∈R)
(1)讨论函数的单调性;
(2)若f(x)≥0恒成立,证明:x1<x2时,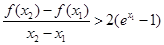
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
(1)求证:AT2=BT·AD;
(2)E、F是BC的三等分点,且DE=DF,求∠A.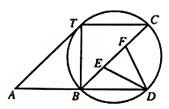
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: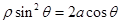 (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为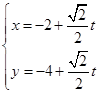 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
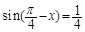 ,则sin2x的值为( )
,则sin2x的值为( )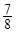
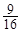
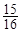
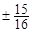
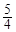
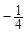
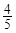
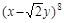 的展开式中
的展开式中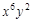 的系数是___________.
的系数是___________.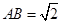 ,点D在边BC上,
,点D在边BC上,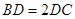 ,
,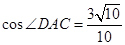 ,
,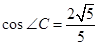 ,则AC+BC=_________________.
,则AC+BC=_________________.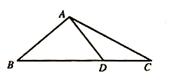
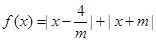 (m>0)
(m>0) 粤公网安备 44130202000953号
粤公网安备 44130202000953号