上海市松江区中考二模数学试卷
已知一组数据x1,x2,x3的平均数和方差分别为6和2,则数据x1+1,x2+1,x3+1的平均数和方差分别是( )
| A.6和2 | B.6和3 | C.7和2 | D.7和3. |
已知在△ABC中,AB=AC=13,BC=10,如果以A为圆心r为半径的⊙A和以BC为直径的⊙D相交,那么r的取值范围( )
| A.3<r<13 | B.5<r<17 | C.7<r<13 | D.7<r<17 |
为了解某区初三学生的课余生活情况,调查小组在全区范围内随机抽取部分学生进行问卷调查.问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图(如图).如果该区有6000名初三学生,请你估计该区最喜欢体育运动的初三学生约有 名.
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知Rt△ABC中,∠B=90°,较短的一条直角边边长为1,如果Rt△ABC是“有趣三角形”,那么这个三角形“有趣中线”长等于
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线A′处,点D落在点D′处,则D′B长为 
如图,已知在△ABC中,AB=AC,BC=8,tan∠ABC=3,AD⊥BC于D,O是AD上一点,OD=3,以OB为半径的⊙O分别交AB、AC于E、F.求:
(1)⊙O的半径;
(2)BE的长.
某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.如图,线段OA和OB分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数w1(张)和每个无人售票窗口售出的车票数w2(张)关于售票时间t(小时)的函数图象.
(1)求w1(张)与t(小时)的函数解析式;
(2)若当天开放无人售票窗口个数是普通售票窗口个数的2倍,从上午8点到上午11点,两种窗口共售出的车票数为2400张,求当天开放无人售票窗口的个数?
如图,在正方形ABCD中,E是边CD上一点,AF⊥AE交CB的延长线于点F,联结DF,分别交AE、AB于点G、P.
(1)求证:AE=AF;
(2)若∠BAF=∠BFD,求证:四边形APED是矩形.
如图,在直角坐标平面内,直线y=-x+5与x轴和y轴分别交于A、B两点,二次函数y=x2+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且△ABP的面积为10,求点P的坐标.
 是同类二次根式的是( )
是同类二次根式的是( )



 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
 的解为
的解为 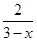 中自变量x的取值范围是
中自变量x的取值范围是  的图象在每个象限内y随x的增大而减小,那么k的取值范围是
的图象在每个象限内y随x的增大而减小,那么k的取值范围是  =
= ,
, =
= ,M是边BC上的一点,BM:CM=1:2,用向量
,M是边BC上的一点,BM:CM=1:2,用向量 =
= 

 ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号