北京市丰台区中考二模数学卷
中国是一个干旱缺水严重的国家,淡水资源总量约为28000亿立方米,约占全球水资源的6%.将28000用科学记数法表示为( )
| A.28×103 | B.2.8×104 | C.2.8×105 | D.0.28×106 |
某班第一小组6名女生在测仰卧起坐时,记录下她们的成绩(单位:个/分):45,48,46,50,50,49.这组数据的平均数是( )
| A.49 | B.48 | C.47 | D.46 |
把代数式ax2-4ax+4a分解因式,下列结果中正确的是( )
| A.a(x-2)2 | B.a(x+2)2 |
| C.a(x-4)2 | D.a(x+2)(x-2) |
如图,在等边△ABC中,BC=6,点D,E分别在AB,AC上,DE∥BC,将△ADE沿DE翻折后,点A落在点A′处.连结A A′并延长,交DE于点M,交BC于点N.如果点A′为MN的中点,那么△ADE的面积为( )
A. |
B.3 |
C.6 |
D.9 |
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为ycm2,那么y与x的函数关系图象可能是( )
A. |
B. |
C. |
D. |
在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是 ,第n个等边三角形的面积是 
已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适.
已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)在x轴的正半轴上存在一点P,且△ABP的面积是6,请直接写出点P的坐标.
某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.
频数分布表
代码和谁一起生活频数频率
A父母42000.7
B爷爷奶奶660a
C外公外婆6000.1
D其它b0.09
合计60001
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD2=CA•CB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA= ,求BE的长.
,求BE的长.
阅读下列材料:
已知:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及此时 的值是多少.
的值是多少.
在解决这个问题时,小明联想到在学习平行线间的距离时所了解的知识:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.进而,小明构造出了如图2的辅助线,并求得PQ的最小值为3.参考小明的做法,解决以下问题:
(1)继续完成阅读材料中的问题:当PQ的长度最小时, = ;
= ;
(2)如图3,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PB为边作□PBQE,那么对角线PQ的最小值为 ,此时 = ;
= ;
(3)如图4,如果P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数),以PE,PC为边作□PCQE,那么对角线PQ的最小值为 ,此时 = .
= .
如图,二次函数y=x2+bx+c经过点(-1,0)和点(0,-3).
(1)求二次函数的表达式;
(2)如果一次函数y=4x+m的图象与二次函数的图象有且只有一个公共点,求m的值和该公共点的坐标;
(3)将二次函数图象y轴左侧部分沿y轴翻折,翻折后得到的图象与原图象剩余部分组成一个新的图象,该图象记为G,如果直线y=4x+n与图象G有3个公共点,求n的值.
如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,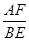 = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6-2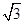 ,求旋转角a的度数.
,求旋转角a的度数.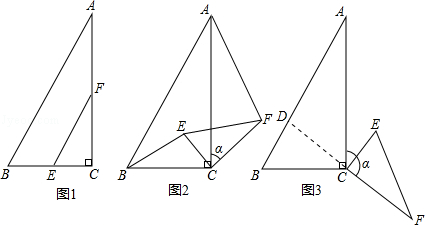
 的相反数是( )
的相反数是( )

 的值为0,那么x的值为 .
的值为0,那么x的值为 .
 -2sin60°+(-2014)0-(
-2sin60°+(-2014)0-( )-1.
)-1. )÷
)÷ 的值.
的值.
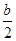 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.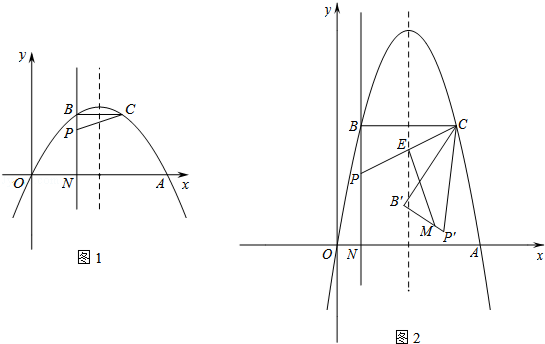
 粤公网安备 44130202000953号
粤公网安备 44130202000953号