北京市昌平区中考一模数学试卷
据统计,第22届冬季奥林匹克运动会的电视转播时间长达88000小时,社交网站和国际奥委会官方网站也创下冬奥会收看率纪录. 用科学计数法表示88000为( )
A. |
B. |
C. |
D. |
抽奖箱里有6个除颜色外其他都相同的U盘,其中1个红色,2个黄色,3个蓝色,摇匀后从中任意摸出一个是黄色的概率为( )
A. |
B. |
C. |
D. |
如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是( )
| A.40° | B.50° | C.70° | D.80° |
学校体育课进行定点投篮比赛,10位同学参加,每人连续投5次,投中情况统计如下:
| 投中球数量(个) |
2 |
3 |
4 |
5 |
| 人数(人) |
1 |
4 |
3 |
2 |
这10位同学投中球数量的众数和中位数分别是( )
A.4, 2 B.3,4 C. 2,3.5 D. 3,3.5
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行. 张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
| A.5.5m | B.6.2m | C.11 m | D.2.2 m |
如图,在△ABC中,AB=AC,tan∠B=2, BC=3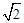 . 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
. 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
A.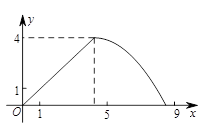 |
B. |
C.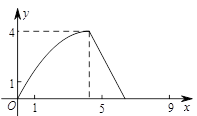 |
D.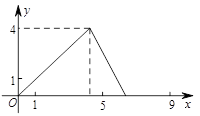 |
如图,已知平行四边形纸片ABCD的周长为20,将纸片沿某条直线折叠,使点D与点B重合,折痕交AD于点E,交BC于点F,连接BE,则△ABE的周长为 . 
已知:四边形ABCD的面积为1. 如图1,取四边形ABCD各边中点,则图中阴影部分的面积为 ;如图2,取四边形ABCD各边三等分点,则图中阴影部分的面积为 ;如图3,取四边形ABCD各边的n(n为大于1的整数)等分点,则图中阴影部分的面积为 .
列方程解应用题:
王亮的父母每天坚持走步锻炼. 今天王亮的妈妈以每小时3千米的速度走了10分钟后,王亮的爸爸刚好看完球赛,马上沿着妈妈所走的路线以每小时4千米的速度追赶,求爸爸追上妈妈时所走的路程.
反比例函数 在第二象限的图象如图所示.
在第二象限的图象如图所示.
(1)直接写出m的取值范围;
(2)若一次函数 的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为
的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为 ,求m的值.
,求m的值.
已知:BD是四边形ABCD的对角线,AB⊥BC,∠C=60°,AB=1,BC= ,CD=
,CD= .
.
(1)求tan∠ABD的值;
(2)求AD的长.

某校为了更好地开展“阳光体育一小时”活动,围绕着“你最喜欢的体育活动项目是什么(只写一项)?”的问题,对本校学生进行了随机抽样调查,以下是根据得到的相关数据绘制的统计图的一部分.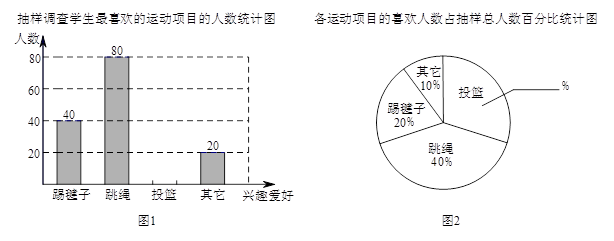
各年级学生人数统计表
| 年级 |
七年级 |
八年级 |
九年级 |
| 学生人数 |
180 |
120 |
|
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢踢毽子运动的人数约为多少?
如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果AC=3,求PD的长.
图1是李晨在一次课外活动中所做的问题研究:他用硬纸片做了两个三角形,分别为△ABC和△DEF,其中∠B=90°,∠A=45°,BC= ,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)请回答李晨的问题:若CD=10,则AD= ;
(2)如图2,李晨同学连接FC,编制了如下问题,请你回答:
①∠FCD的最大度数为 ;
②当FC∥AB时,AD= ;
③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边时,AD= ;
④△FCD的面积s的取值范围是 .
如图,已知二次函数 (a≠0)的图象经过点A,点B.
(a≠0)的图象经过点A,点B.
(1)求二次函数的表达式;
(2)若反比例函数 (x>0)的图象与二次函数
(x>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,
, 落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
(3)若反比例函数 (x>0,k>0)的图象与二次函数
(x>0,k>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,且
,且 ,试求实数k的取值范围.
,试求实数k的取值范围.
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD 的度数;
(3)如图3,如果 =45°,AB =2,AE=
=45°,AB =2,AE= ,求点G到BE的距离.
,求点G到BE的距离.
 的倒数是( )
的倒数是( )







 分解因式,结果为 .
分解因式,结果为 . .
.
 .
. ,求
,求 的值.
的值. 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号