江苏省扬州市高二下学期期末考试文科数学试卷
“ ”是“函数
”是“函数 为奇函数”的 条件.
为奇函数”的 条件.
(从“充要”,“充分不必要”,“必要不充分”,“既不充分也不必要”中选择适当的填写)
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
已知函数 是定义在
是定义在 上的单调增函数,且对于一切实数x,不等式
上的单调增函数,且对于一切实数x,不等式 恒成立,则实数b的取值范围是 .
恒成立,则实数b的取值范围是 .
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:(i)
满足:(i) ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .那么称这两个集合“保序同构”.现给出以下4对集合.①
.那么称这两个集合“保序同构”.现给出以下4对集合.① ;②
;② ;③
;③ ;④
;④ ,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
已知 ,命题
,命题 ,命题
,命题 .⑴若命题
.⑴若命题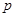 为真命题,求实数
为真命题,求实数 的取值范围;⑵若命题
的取值范围;⑵若命题 为真命题,命题
为真命题,命题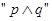 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
已知函数 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
⑵设 ,且函数
,且函数 为偶函数,求证:
为偶函数,求证: .
.
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数 ,
, 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A, 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
如图,圆 与坐标轴交于点
与坐标轴交于点 .
.
⑴求与直线 垂直的圆的切线方程;
垂直的圆的切线方程;
⑵设点 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线 交
交 轴于点
轴于点 ,直线
,直线 交直线
交直线 于点
于点 ,
,
①若 点坐标为
点坐标为 ,求弦
,求弦 的长;②求证:
的长;②求证: 为定值.
为定值.
来源:2013-2014学年江苏省扬州市高二下学期期末考试文科数学试卷
 ,集合
,集合 ,则
,则 .
. 为虚数单位,复数
为虚数单位,复数 = .
= . 的定义域为 .
的定义域为 . 在
在 处的切线的斜率为 .
处的切线的斜率为 . +
+ =4则sin2
=4则sin2 的坐标为 .
的坐标为 . 的值域为 .
的值域为 . ,则
,则 .
. 的图象与函数
的图象与函数 的图象恰有两个交点,则实数
的图象恰有两个交点,则实数 的取值范围是 .
的取值范围是 . ,若分别以
,若分别以 为弦作两外切的圆
为弦作两外切的圆 和圆
和圆 ,且两圆半径相等,则圆的半径为 .
,且两圆半径相等,则圆的半径为 . 的不等式
的不等式 的解集中的正整数解有且只有3个,则实数
的解集中的正整数解有且只有3个,则实数 的取值范围是 .
的取值范围是 . 的最小正周期为
的最小正周期为 .
. 的对称轴方程;
的对称轴方程; ,
, ,求
,求 的值.
的值. ,函数
,函数 .
. 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值; 时,试判断函数
时,试判断函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号