福建省四地六校高二下学期第一次月考文科数学试卷
下列表示图书借阅的流程正确的是( )
A.入库 阅览 阅览 借书 借书 找书 找书 出库 出库 还书 还书 |
B.入库 找书 找书 阅览 阅览 借书 借书 出库 出库 还书 还书 |
C.入库 阅览 阅览 借书 借书 找书 找书 还书 还书 出库 出库 |
D.入库 找书 找书 阅览 阅览 借书 借书 还书 还书 出库 出库 |
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 |
B.模型2的相关指数 为0.86 为0.86 |
C.模型3的相关指数 为0.68 为0.68 |
D.模型4的相关指数 为0.58 为0.58 |
某商品销售量 (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )
A. |
B. |
C. |
D. |
设抛物线 上一点P到
上一点P到 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )
| A.12 | B.8 | C.6 | D.4 |
按流程图的程序计算,若开始输入的值为 =2,则输出的
=2,则输出的 的值是( )
的值是( )
| A.3 | B.6 | C.21 | D.156 |
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
观察 ,
, ,
, ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数 满足
满足 ,记
,记 为
为 的导函数,则
的导函数,则 =( )
=( )
A. |
B. |
C. |
D. |
把正整数按右图所示的规律排序,则从2013到2015的箭头方向依次为( )
A. |
B. |
C. |
D. |
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如表.预计在今后的销售中,销量与单价仍然服从 (
(  ,
, )的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
)的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
A. B.8 C.
B.8 C. D.
D.
已知抛物线 :
: 与点
与点 ,过
,过 的焦点且斜率为
的焦点且斜率为 的直线与
的直线与 交于
交于 ,
, 两点,若
两点,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
在平面上,我们用一直线去截正方形的一个角,那么截下的一个直角三角形,按如图所标边长,由勾股定理有 .设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,如果用
,如果用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么类比得到的结论是 .
表示截面面积,那么类比得到的结论是 .
已知复数 ,
, .
.
(1)若 为纯虚数,求实数
为纯虚数,求实数 的值;
的值;
(2)当 =1时,若
=1时,若 ,请问复数
,请问复数 在复平面内对应的点在第几象限?
在复平面内对应的点在第几象限?
为调查某市老年人是否需要志愿者提供帮助,用简单随机抽样方法从该市调查了500位老年人,结果如右表.
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该市老年人中, 需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关?
附:
 (
( )
)
 |
0.050 |
0.010 |
0.001 |
 |
3.841 |
6.635 |
10.828 |
已知函数 .
.
(1)求 的极值(用含
的极值(用含 的式子表示);
的式子表示);
(2)若 的图象与
的图象与 轴有3个不同交点,求
轴有3个不同交点,求 的取值范围.
的取值范围.
已知A= ,B=
,B= ,C=
,C=
(1)试分别比较A与B、B与C的大小(只要写出结果,不要求证明过程);
(2)根据(1)的比较结果,请推测出 与
与 (
( )的大小,并加以证明.
)的大小,并加以证明.
已知函数 (
( ).
).
(1)求函数 的单调区间;
的单调区间;
(2)请问,是否存在实数 使
使 上恒成立?若存在,请求实数
上恒成立?若存在,请求实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 是虚数单位,复数
是虚数单位,复数 ,则
,则 =( )
=( )




 ,
, (
( 为虚数单位),则
为虚数单位),则 的值为 .
的值为 . 的两条渐近线的方程为 .
的两条渐近线的方程为 .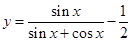 在点
在点 处的切线的斜率为 .
处的切线的斜率为 . :
: 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆
过椭圆 .
. 过椭圆
过椭圆 ,交椭圆于点P、Q.
,交椭圆于点P、Q. (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积; 在
在 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点
的一条角平分线,则称点 粤公网安备 44130202000953号
粤公网安备 44130202000953号