在平面上，我们用一直线去截正方形的一个角，那么截下的一个直角三角形，按如图所标边长，由勾股定理有
．设想正方形换成正方体，把截线换成如图截面，这时从正方体上截下三条侧棱两两垂直的三棱锥
，如果用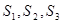
表示三个侧面面积，
表示截面面积，那么类比得到的结论是 ．
在
处取极值，则a＝________.
，若
是奇函数，则
+
的值为 
，
，
，
；
，
，
，
的分解式中的第三个数为 ____．
，y＝2－x，y＝－
x所围成图形的面积为_______。
在区间（-1,1）上恰有一个极值点，则实数
的取值范围是____．相关知识点
推荐套卷
在平面上，我们用一直线去截正方形的一个角，那么截下的一个直角三角形，按如图所标边长，由勾股定理有．设想正方形换成正方体，把截线换成如图截面，这时从正方体上截下三条侧棱两两垂直的三棱锥，如果用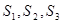表示三个侧面面积，表示截面面积，那么类比得到的结论是 ．
粤公网安备 44130202000953号