广东省东莞市高三第二次模拟考试文科数学试卷
对于非零向量 、
、 ,“
,“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届广东省东莞市高三第二次模拟考试文科数学试卷
如图是 年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
A. |
B. |
C. |
D. |

来源:2014届广东省东莞市高三第二次模拟考试文科数学试卷
已知 、
、 是两条直线,
是两条直线, 、
、 是两个平面,给出下列命题:①若
是两个平面,给出下列命题:①若 ,
, ,则
,则 ;②若平面
;②若平面 上有不共线的三点到平面
上有不共线的三点到平面 的距离相等,则
的距离相等,则 ;③若
;③若 、
、 为异面直线,
为异面直线, ,
, ,
, ,
, ,则
,则 .其中正确命题的个数( )
.其中正确命题的个数( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
来源:2014届广东省东莞市高三第二次模拟考试文科数学试卷
(本小题满分12分)一工厂生产甲、乙、丙三种样式的杯子,每种样式均有 和
和 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取
两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取 个,其中有甲样式杯子
个,其中有甲样式杯子 个.
个.
| 型号 |
甲样式 |
乙样式 |
丙样式 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)求 的值;
的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为 的样本,从这个样本中任取
的样本,从这个样本中任取 个杯子,求至少有
个杯子,求至少有 个
个 杯子的概率.
杯子的概率.
来源:2014届广东省东莞市高三第二次模拟考试文科数学试卷
如图,已知 平面
平面 ,
, ,
, ,
,
且 是
是 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求此多面体的体积.
来源:2014届广东省东莞市高三第二次模拟考试文科数学试卷
 ,
, ,则下列关系中正确的是( )
,则下列关系中正确的是( )



 的虚部是( )
的虚部是( )



 的图象与
的图象与 的图象关于直线
的图象关于直线 对称,则
对称,则 ( )
( )



 、
、 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )



 的右焦点与抛物线
的右焦点与抛物线 焦点重合,则此双曲线的渐近线方程是( )
焦点重合,则此双曲线的渐近线方程是( )



 ,则点
,则点 必在( )
必在( ) 的左下方
的左下方 的右上方
的右上方 、
、 、
、 是圆
是圆 上的三点,
上的三点, 的延长线与线段
的延长线与线段 交于圆内一点
交于圆内一点 ,若
,若
 ,则 ( )
,则 ( )




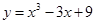 的极小值是 .
的极小值是 . 是等差数列,
是等差数列, ,
, ,则首项
,则首项 .
.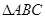 的内角
的内角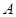 、
、 、
、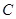 所对的边分别为
所对的边分别为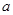 、
、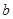 、
、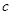 ,且
,且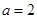 ,
,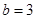 ,
,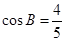 .
.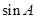 的值为 .
的值为 . (
( 为参数)的倾斜角是
为参数)的倾斜角是  的割线
的割线 交圆
交圆 、
、 两点,割线
两点,割线 经过圆心
经过圆心 ,
, ,
, ,则圆
,则圆
 ,
, .
.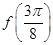 的值;
的值; 的最大值和最小正周期;
的最大值和最小正周期; ,
,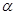 是第二象限的角,求
是第二象限的角,求 .
. ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上. ;
; ,证明:
,证明: .
. .
. 时,求函数
时,求函数 的极值;
的极值; ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 的离心率为
的离心率为 ,以椭圆
,以椭圆 的
的 为圆心作圆
为圆心作圆 ,设圆
,设圆 与点
与点 .
. 的最小值,并求此时圆
的最小值,并求此时圆 是椭圆
是椭圆 、
、 分别与
分别与 轴交于点
轴交于点 、
、 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号