2011年全国统一高考理科数学试卷(陕西卷)
函数 在 内()
| A. | 没有零点 | B. | 有且仅有一个零点 |
| C. | 有且仅有两一个零点 | D. | 有无穷个零点 |
如图中, 为某次考试三个评阅人对同一道题的独立评分, 为该题的最终得分,当 时 等于()
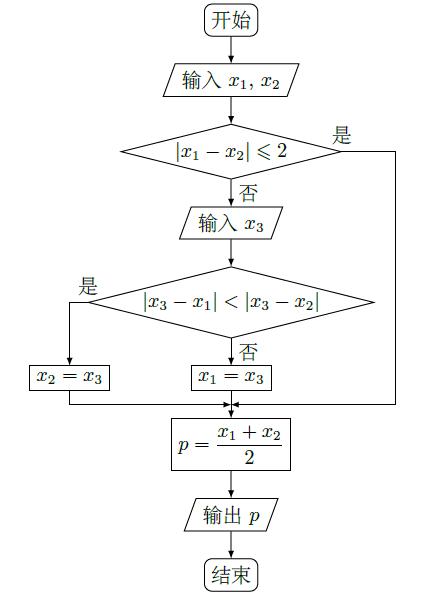
| A. | 11 | B. | 10 | C. | 8 | D. | 7 |
设 是变量 和 的 个样本点,直线 是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是

| A. | 和 相关系数为直线l的斜率 |
| B. | 和 的相关系数在0到1之间 |
| C. | 当 为偶数时,分布在l两侧的样本点的个数一定相同 |
| D. | 直线 过点 |
甲乙两人一起去"2011西安世园会",他们约定,各自独立地从1到6号景点中任意选4个进行浏览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是()
| A. |
|
B. |
|
C. |
|
D. |
|
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
......
照此规律,第
个等式为
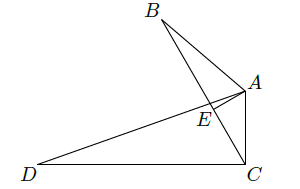
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米,开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为(米)。
(坐标系与参数方程选做题)在直角坐标系 中,以原点为极点, 轴正半轴为极轴建立极坐标系,设点 分别在曲线 和曲线 上,则 的最小值为.
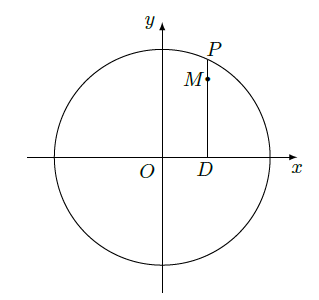
如图,设
是圆珠笔
上的动点,点
是
在
轴上的投影,
为
上一点,且
(Ⅰ)当
的在圆上运动时,求点
的轨迹
的方程;
(Ⅱ)求过点
且斜率为
的直线被
所截线段的长度.
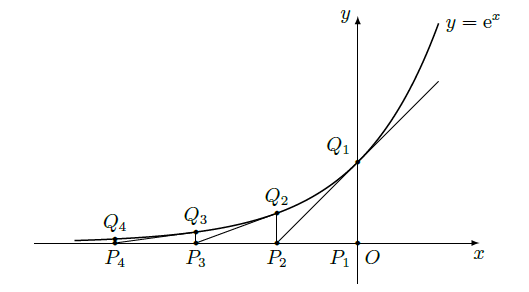
如图,从点 作 轴的垂线交曲线 于点 ,曲线在 点处的切线与 轴交于点 ,再从 作 轴的垂线交曲线于点 ,依次重复上述过程得到一系列点: ,记 点的坐标为 .
(Ⅰ)试求
与
的关系(
)
(Ⅱ)求
如图,A地到火车站共有两条路径
和
,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) |
|||||
|
的频率 |
0.1 |
0.2 |
0.3 |
0.2 |
0.2 |
|
的频率 |
0 |
0.1 |
0.4 |
0.4 |
0.1 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站。
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用
表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求
的分布列和数学期望。
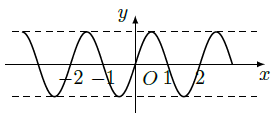
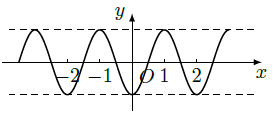

 粤公网安备 44130202000953号
粤公网安备 44130202000953号