山东省菏泽市高三3月模拟考试文科数学试卷
下列命题中的真命题是( )
A.对于实数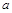 、b、c,若 、b、c,若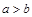 ,则 ,则 |
| B.x2>1是x>1的充分而不必要条件 |
C. ,使得 ,使得 成立 成立 |
D. , ,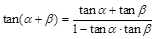 成立 成立 |
某几何体的三视图如图所示,且该几何体的体积是 ,则正视图中的
,则正视图中的 的值是( )
的值是( )
| A.2 | B.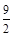 |
C. |
D. 3 |
某程序框图如图2所示,现将输出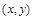 值依次记为:
值依次记为: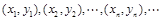 若程序运行中输出的一个数组是
若程序运行中输出的一个数组是 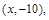 则数组中的
则数组中的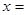 ( )
( )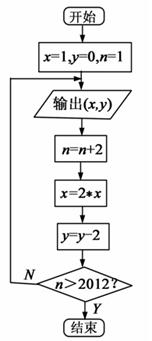
| A.32 | B.24 | C.18 | D.16 |
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
| |
做不到“光盘” |
能做到“光盘” |
| 男 |
45 |
10 |
| 女 |
30 |
15 |
附:
P(K2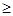 k) k) |
0.10 |
0.05 |
0.025 |
| k |
2.706 |
3.841 |
5.024 |

参照附表,得到的正确结论是( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
已知函数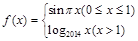 ,若a、b、c互不相等,且
,若a、b、c互不相等,且 ,则a+b+c的取值范围是( )
,则a+b+c的取值范围是( )
| A.(1,2014) | B.(1,2015) | C.(2,2015) | D.[2,2015] |
已知抛物线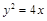 的准线过双曲线
的准线过双曲线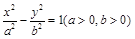 的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为
的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B.4 | C.3 | D.2 |
如图,A是半径为5的圆O上的一个定点,单位向量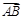 在A点处与圆O相切,点P是圆O上的一个动点,且点P与点A不重合,则
在A点处与圆O相切,点P是圆O上的一个动点,且点P与点A不重合,则 ·
·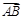 的取值范围是
的取值范围是 
函数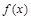 的定义域为A,若
的定义域为A,若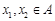 且
且 时总有
时总有 ,则称
,则称 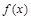 为单函数.例如,函数
为单函数.例如,函数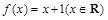 是单函数.下列命题:
是单函数.下列命题:
①函数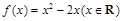 是单函数;②函数
是单函数;②函数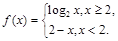 是单函数;
是单函数;
③若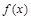 为单函数,
为单函数, 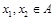 且
且 ,则
,则 ;
;
④若函数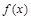 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则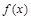 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
已知函数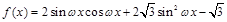 (
( )的最小正周期为
)的最小正周期为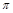 .
.
(1)求函数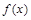 的单调增区间;
的单调增区间;
(2)将函数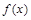 的图象向左平移
的图象向左平移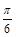 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象;若
的图象;若 在
在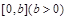 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证: EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 |
[80,85) |
[85,90) |
[90,95) |
[95,100] |
| 件数 |
5 |
a |
15 |
b |
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
已知数列{an}, ,
, ,记
,记 ,
, ,
, ,若对于任意
,若对于任意 ,A(n),B(n),C(n)成等差数列.
,A(n),B(n),C(n)成等差数列.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和.
 ,
, ,则
,则 ( )
( )



 ,则( )
,则( )
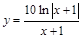 的图象可能是( )
的图象可能是( )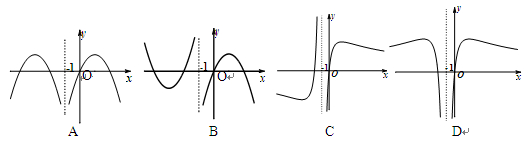
 满足
满足 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )



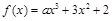 ,若f (x)在x=1处的切线与直线
,若f (x)在x=1处的切线与直线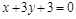 垂直,则实数a的值为
垂直,则实数a的值为 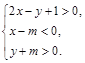 表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是 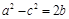 ,且
,且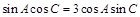 ,
,
 时,求函数
时,求函数 的极值;
的极值; 没有零点,求实数a取值范围.
没有零点,求实数a取值范围. 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程; 轴交于点R,S,O为坐标原点。求证:
轴交于点R,S,O为坐标原点。求证: 为定值.
为定值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号