广东省肇庆市高三3月第一次模拟理科数学试卷
已知全集U={-2,-1,0,1,2,3,4,5,6},集合M={大于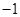 且小于4的整数},则
且小于4的整数},则 ( )
( )
A. |
B.{-2,-1,5,6} |
| C.{0,1,2,3,4} | D.{-2,-1,4,5,6} |
若如图所示的程序框图输出的S是30,则在判断框中M表示的“条件”应该是( )
A. |
B. |
C. |
D. |
下列命题中,真命题是 ( )
A. , , ; ; |
B. , , ; ; |
C.“ ”是“ ”是“ ”的充分不必要条件; ”的充分不必要条件; |
D.设 , , 为向量,则“ 为向量,则“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
设向量 ,
, ,定义一种向量积:
,定义一种向量积: .已知向量
.已知向量 ,
, ,点P在
,点P在 的图象上运动,点Q在
的图象上运动,点Q在 的图象上运动,且满足
的图象上运动,且满足 (其中O为坐标原点),则
(其中O为坐标原点),则 在区间
在区间 上的最大值是( )
上的最大值是( )
| A.4 | B.2 | C. |
D. |
已知集合A={4},B={1,2},C={1,3,5},从这三个集合中各取一个元素构成空间直角坐标系中的点的坐标,则确定的不同点的个数为 .
已知曲线C的极坐标方程为 (
( ),曲线C在点(2,
),曲线C在点(2, )处的切线为l,以极点为坐标原点,以极轴为x轴的正半轴建立直角坐标系,则l的直角坐标方程为 .
)处的切线为l,以极点为坐标原点,以极轴为x轴的正半轴建立直角坐标系,则l的直角坐标方程为 .
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: ,2;
,2; ,7;
,7; ,10;
,10; ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中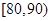 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为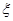 ,求
,求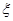 的数学期望.
的数学期望.
如图,在直三棱柱 中,D、E分别是BC和
中,D、E分别是BC和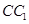 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.

(1)求证: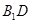 ⊥平面
⊥平面 ;
;
(2)求二面角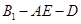 的余弦值;
的余弦值;
(3)求三棱锥 的体积.
的体积.
已知数列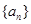 的前n项和为
的前n项和为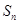 ,且满足
,且满足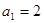 ,
,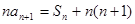 .
.
(1)求数列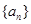 的通项公式
的通项公式 ;
;
(2)设 为数列{
为数列{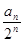 }的前n项和,求
}的前n项和,求 ;
;
(3)设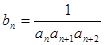 ,证明:
,证明: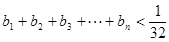 .
.
设双曲线C: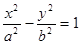 (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为(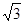 ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
 ,
, ,
, ,
, 中,偶函数的个数是( )
中,偶函数的个数是( ) 是虚数单位,
是虚数单位, ,
, 为复数
为复数 的共轭复数,则
的共轭复数,则 ( )
( )



 的展开式中
的展开式中 的系数是( )
的系数是( )





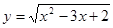 的定义域为 .
的定义域为 . 在
在 处的切线方程为 .
处的切线方程为 . 满足
满足 ,则
,则 .
. 所表示的平面区域内一动点,则线段|OP|的最小值等于 .
所表示的平面区域内一动点,则线段|OP|的最小值等于 . ,则DC= .
,则DC= .
 ,
,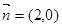 ,
, ,函数
,函数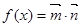 .
. 的表达式;
的表达式; 的值;
的值;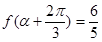 ,
,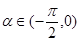 ,求
,求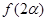 的值.
的值.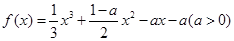 .
. 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围; 粤公网安备 44130202000953号
粤公网安备 44130202000953号