山东省烟台市高三统一质量检测考试理科数学试卷
已知集合M={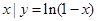 },集合N={
},集合N={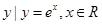 },(e为自然对数的底数)则
},(e为自然对数的底数)则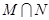 =( )
=( )
A.{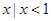 } } |
B.{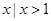 } } |
C.{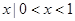 } } |
D.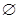 |
一个空间几何体的三视图如下左图所示,则该几何体的表面积为( )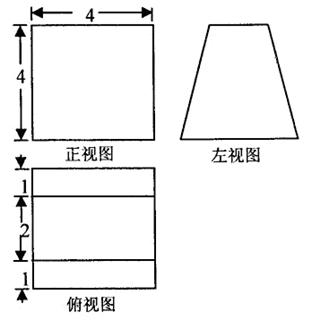
| A.48 | B.48+8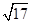 |
C.32+8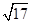 |
D.80 |
某程序的框图如上右图所示,执行该程序,若输入的p为l6,则输出的n的值为( )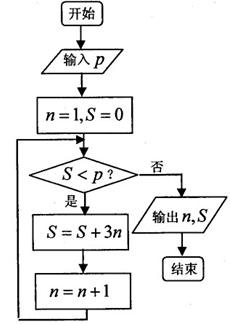
| A.3 | B.4 | C.5 | D.6 |
以q为公比的等比数列{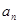 }中,
}中,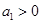 ,则“
,则“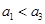 ”是“
”是“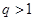 ”的( )
”的( )
| A.必要而不充分条件 | B.充分而不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知不重合的直线m、l和平面 ,且
,且 ,
, .给出下列命题:
.给出下列命题:
①若 ,则
,则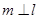 ;
;
②若 ,则
,则 ;
;
③若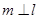 ,则
,则 ;
;
④若 ,则
,则 ,
,
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知圆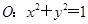 及以下三个函数:①
及以下三个函数:①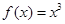 ;②
;②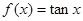 ;③
;③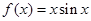 .其中图象能等分圆
.其中图象能等分圆 面积的函数个数为( )
面积的函数个数为( )
| A.3 | B.2 | C.1 | D.0 |
双曲线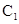 的中心在原点,焦点在x轴上,若
的中心在原点,焦点在x轴上,若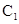 的一个焦点与抛物线
的一个焦点与抛物线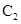 :
: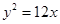 的焦点重合,且抛物线
的焦点重合,且抛物线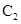 的准线交双曲线
的准线交双曲线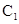 所得的弦长为4
所得的弦长为4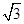 ,则双曲线
,则双曲线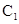 的实轴长为( )
的实轴长为( )
| A.6 | B.2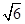 |
C.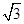 |
D.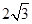 |
有6人入住宾馆中的6个房间,其中的房号301与302对门,303与304对门,305与306对门,若每人随机地拿了这6个房间中的一把钥匙,则其中的甲、乙两人恰好对门的概率为 .
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集D={a|a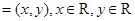 }上也可以定义一个称为“序”的关系,记为“
}上也可以定义一个称为“序”的关系,记为“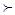 ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 ,
, 

 ,当且仅当“
,当且仅当“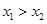 ”或“
”或“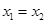 且
且 ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若 则
则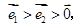
② ,
, ,则
,则 ;
;
③若 ,则对于任意
,则对于任意 ,
, 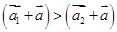 ;
;
④对于任意向量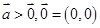 ,若
,若 ,则
,则 .
.
其中真命题的序号为 .
已知m=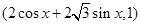 ,n=
,n= ,满足
,满足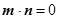 .
.
(1)将y表示为x的函数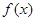 ,并求
,并求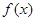 的最小正周期;
的最小正周期;
(2)已知a,b,c分别为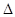 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长,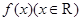 的最大值是
的最大值是 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.
已知数列{an}前n项和为Sn,首项为a1,且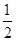 ,an,Sn成等差数列.
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)数列{bn}满足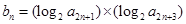 ,求证:
,求证: .
.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大。我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某市环保局从360天的市区PM2.5监测数据中,随机抽取l5天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).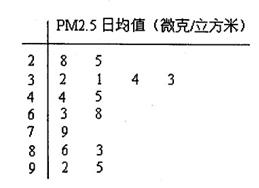
(1)从这l5天的数据中任取3天的数据,记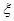 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求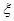 的分布列;
的分布列;
(2)以这l5天的PM2.5日均值来估计这360天的空气质量情况,则其中大约有多少天的空气质量达到一级.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿直线BD将△BCD翻折成△BC D,使得平面BC
D,使得平面BC D
D 平面ABD.
平面ABD.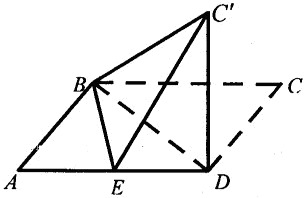
(1)求证:C'D 平面ABD;
平面ABD;
(2)求直线BD与平面BEC'所成角的正弦值.
已知椭圆C的中点在原点,焦点在x轴上,离心率等于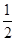 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线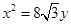 的焦点.
的焦点.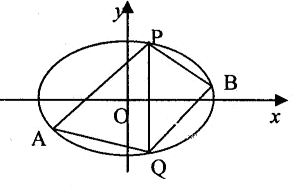
(1)求椭圆C的方程;
(2)己知点P(2,3),Q(2,-3)在椭圆上,点A、B是椭圆上不同的两个动点,且满足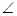 APQ=
APQ=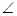 BPQ,试问直线AB的斜率是否为定值,请说明理由.
BPQ,试问直线AB的斜率是否为定值,请说明理由.
 的虚部为( )
的虚部为( )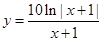 图象的是( )
图象的是( )
 ,且
,且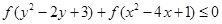 ,则当
,则当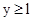 时,
时,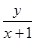 的取值范围是( )
的取值范围是( )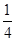 ,
,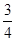 ]
] ]
] ,则
,则 的最小值是 .
的最小值是 . ,则
,则 = .
= . ,则二项式
,则二项式 的展开式中含有
的展开式中含有 的项是 .
的项是 .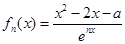 ,其中
,其中 N*,a
N*,a R,e是自然对数的底数.
R,e是自然对数的底数.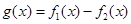 的零点;
的零点; N*,
N*,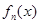 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;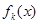 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性. 粤公网安备 44130202000953号
粤公网安备 44130202000953号