人教版高考数学文科二轮专题复习提分训练23练习卷

已知向量a=(1,m),b=(m,2),若a∥b,则实数m等于(　　)

A．-	B．
C．-或	D．0

已知点A(1,3),B(4,-1),则与向量同方向的单位向量为(　　)

A．	B．
C．	D．

已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为(　　)

A．-1	B．
C．+1	D．+2

若向量=(1,2),=(3,4),则等于(　　)

设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|等于(　　)

A．

B．

C．2

D．10

已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ等于(　　)

A．

B．

C．1

D．2

设向量a,b满足|a|=2,b=(2,1),且a与b的方向相反,则a的坐标为　　　.

在四边形ABCD中,=(1,2),=(-4,2),则该四边形的面积为(　　)

A．

B．2

C．5

D．10

设向量a,b满足|a|=|b|=1,a·b=-,则|a+2b|等于(　　)

A．

B．

C．

D．

若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为(　　)

若a,b是非零向量,且a⊥b,|a|≠|b|,则函数f(x)=(xa+b)·(xb-a)是(　　)

在OA为边,OB为对角线的矩形中,=(-3,1),=(-2,k),则实数k=　　　.

已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b,若b·c=0,则t=　　　　.

设e₁,e₂为单位向量,非零向量b=xe₁+ye₂,x,y∈R.若e₁,e₂的夹角为,则的最大值等于　　　　.

已知正方形ABCD的边长为2,E为CD的中点,则·=　　　　.

若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为　　　　.

在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若·=1,则AB的长为　　　　.

在△ABC中,M是线段BC的中点,AM=3,BC=10,则·=　　　　.

如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=3,则·=　　　　.

已知向量a,b夹角为45°,且|a|=1,|2a-b|=,则|b|=　　　　.

已知点A(-1,1)、B(1,2)、C(-2,-1)、D(3,4),则向量在方向上的投影为(　　)

A．

B．

C．-

D．-

已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ等于(　　)

已知向量a=(1,k),b=(2,2),且a+b与a共线,那么a·b的值为(　　)

若向量a=(1,2),b=(1,-1),则2a+b与a-b的夹角等于(　　)

A．-

B．

C．

D．

若向量a=(1,1),b=(2,5),c=(3,x),满足条件(8a-b)·c=30,则x等于(　　)

在平面直角坐标系xOy中,已知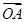="(-1,t)," 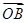=(2,2),若∠ABO=90°,则实数t的值为　　　　.

设向量a=(1,2m),b=(m+1,1),c=(2,m).若(a+c)⊥b,则|a|=　　　　.

若向量a=(1,1),b=(-1,2),则a·b等于　　　.

设向量a=(sin x,sin x),b="(cos" x,sin x),x∈.
(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.

已知向量a="(cos" α,sin α),b="(cos" β,sin β),0<β<α<π.
(1)若|a-b|=,求证:a⊥b;
(2)设c=(0,1),若a+b=c,求α,β的值.

在平面直角坐标系xOy中,已知点A(-1,-2),B(2,3),C(-2,-1).
(1)求以线段AB、AC为邻边的平行四边形的两条对角线的长;
(2)设实数t满足(-t)·=0,求t的值.

设向量a=(1,-3),b=(-2,4),若表示向量4a,3b-2a,c的有向线段首尾相接能构成三角形,则向量c为(　　)

设="(1,-2)," ="(a,-1)," =(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则+的最小值为　　　　.

若·+<0,则△ABC必定是(　　)

已知在△ABC中,AB=AC=4,BC=4,点P为边BC所在直线上的一个动点,则关于·(+)的值,下列选项正确的是(　　)

若a、b是两个非零向量,且|a|=|b|=λ|a+b|,λ∈,则b与a-b的夹角的取值范围是　　　　.

在△ABC中,=(cos18°,cos72°),=(2cos63°,2cos27°),则△ABC面积为(　　)

A．

B．

C．

D．

已知向量a="(1,2),b=(cos" α,sin α),设m=a+tb(t为实数).
(1)若α=,求当|m|取最小值时实数t的值;
(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m夹角的余弦值为,若存在,请求出t;若不存在,请说明理由.

设点G是△ABC的重心,若∠A="120°," ·=-1,则||的最小值是(　　)

A．	B．
C．	D．

已知A(3,),O是原点,点P(x,y)的坐标满足则的取值范围为　　　　.