山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
某中学高中一年级有 人,高中二年级有
人,高中二年级有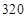 人,高中三年级有
人,高中三年级有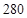 人,现从中抽取一个容量为
人,现从中抽取一个容量为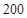 人的样本,则高中二年级被抽取的人数为( )
人的样本,则高中二年级被抽取的人数为( )
A.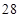 |
B.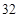 |
C.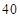 |
D.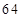 |
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
设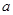 、
、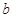 是两条不同的直线,
是两条不同的直线,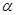 、
、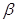 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若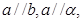 则 则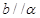 |
B.若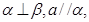 则 则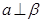 |
C.若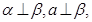 则 则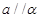 |
D.若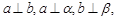 则 则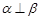 |
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
在实验室进行的一项物理实验中,要先后实施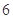 个程序,其中程序
个程序,其中程序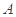 只能出现在第一或最后一步,程序
只能出现在第一或最后一步,程序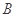 和
和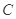 在实施时必须相邻,则实验顺序的编排方法共有( )
在实施时必须相邻,则实验顺序的编排方法共有( )
A.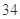 种 种 |
B.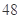 种 种 |
C.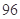 种 种 |
D.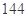 种 种 |
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
如图,从点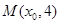 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线 上的点
上的点 ,经直线反射后又回到点
,经直线反射后又回到点 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D.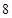 |
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
如果对定义在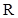 上的函数
上的函数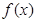 ,对任意两个不相等的实数
,对任意两个不相等的实数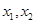 ,都有
,都有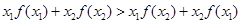 ,则称函数
,则称函数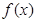 为“
为“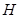 函数”.给出下列函数①
函数”.给出下列函数①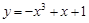 ;②
;②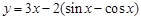 ;③
;③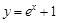 ;④
;④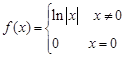 .
.
以上函数是“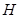 函数”的所有序号为 .
函数”的所有序号为 .
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
已知向量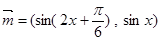 ,
,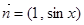 ,
,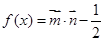 .
.
(1)求函数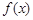 的单调递减区间;
的单调递减区间;
(2)在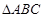 中,
中,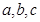 分别是角
分别是角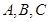 的对边,
的对边,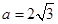 ,
,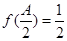 ,
,
若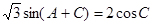 ,求
,求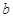 的大小.
的大小.
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
袋中装有大小相同的黑球和白球共 个,从中任取
个,从中任取 个都是白球的概率为
个都是白球的概率为 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取 个球,取出的球不放回,直到其中有一人取到白球时终止.用
个球,取出的球不放回,直到其中有一人取到白球时终止.用 表示取球终止时取球的总次数.
表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布及数学期望
的概率分布及数学期望 .
.
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
如图,四棱锥 中,
中, 面
面 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点,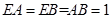 ,
, .
.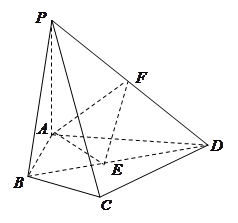
(1)证明: ∥面
∥面 ;
;
(2)求面 与面
与面 所成锐角的余弦值.
所成锐角的余弦值.
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
在数列
 中,其前
中,其前 项和为
项和为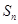 ,满足
,满足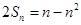 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设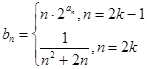 (
(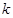 为正整数),求数列
为正整数),求数列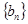 的前
的前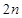 项和
项和 .
.
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
已知函数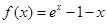 .
.
(1)求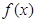 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设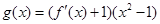 ,试问函数
,试问函数 在
在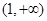 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
来源:2014届山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷
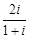 (
(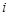 是虚数单位)的虚部为( )
是虚数单位)的虚部为( )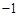
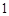
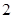
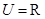 ,集合
,集合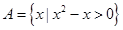 ,
,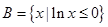 ,则
,则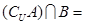 ( )
( )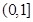
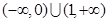
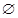
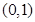
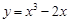 在
在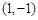 处的切线方程为( )
处的切线方程为( )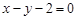
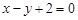
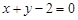
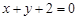
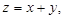 其中实数
其中实数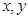 满足
满足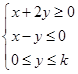 ,若
,若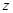 的最大值为
的最大值为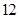 ,则
,则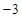
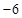
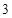
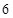
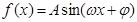
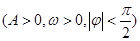 的部分图象如图所示,若
的部分图象如图所示,若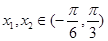 ,且
,且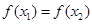 ,则
,则 ( )
( )
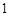
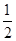
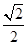
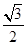
 的图象大致是( )
的图象大致是( )
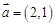 ,
,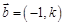 ,若
,若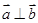 ,则实数
,则实数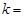 ______;
______;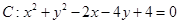 的圆心到直线
的圆心到直线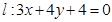 的距离
的距离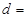 ;
; 中的实数
中的实数 ,则输出的
,则输出的 的概率为 ;
的概率为 ; 
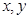 均为正实数,且
均为正实数,且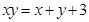 ,则
,则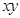 的最小值为__________;
的最小值为__________; ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 ,
, 两点,
两点,  的距离为
的距离为 ,连接椭圆
,连接椭圆 .
. ,设
,设 是椭圆
是椭圆 两点的直线
两点的直线 交
交 轴于点
轴于点 ,若
,若 , 求
, 求 的取值范围;
的取值范围; 与椭圆
与椭圆 ,
, ,其中
,其中 ,若点
,若点 是线段
是线段 垂直平分线上一点,且满足
垂直平分线上一点,且满足 ,求实数
,求实数 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号