湖北省武汉市高三调研测试数学文卷
已知a、b为非零向量, ,若
,若 ,当且仅当t=
,当且仅当t= 时,|m|取得最小值,则向量a,b的夹角为
时,|m|取得最小值,则向量a,b的夹角为
A. |
B. |
C. |
D. |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
若变量x,y满足约束条件 则目标函数Z==x+2y的取值范围是
则目标函数Z==x+2y的取值范围是
| A.[2,6] | B.[2,5] | C.[3,6] | D.[3,5] |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
某学校对高二年级一次考试进行抽样分析.右图是根据抽样分析后的考试成绩绘制的频率分布直方图,其中抽样成绩的范围是[96,106],样本数据分组为[%,兇),[98,100),[100,102),[102,104),[ 104,106].已知样本中成绩小于100分的人数是36,则样本中成绩大于或等于98分且小于 104分的人数
104分的人数 是
是
| A.90 | B.75 | C.60 | D.45 |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
将4名志愿者分配到3所不同的学校进行学生课外活动内容调查,每个学校至少分配一名志愿者的方案种数为
| A.24 | B.36 | C.72 | D.144 |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
在正方体 中,M为
中,M为 的中
的中 点,0为底面ABCD的中心,P为棱
点,0为底面ABCD的中心,P为棱 的中点,则直线OP与直线AM所成的角是
的中点,则直线OP与直线AM所成的角是
A. |
B. |
C. |
D. |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
已知函数, ’若
’若 在(0,
在(0, )上单调递减,则实数a的取值范围为
)上单调递减,则实数a的取值范围为
A.(0, ) ) |
B.(0, ] ] |
C.[ ) ) |
D.( ,1) ,1) |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
已知 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在一点P,满足了
的左、右焦点,若在双曲线右支上存在一点P,满足了 ,且直线PF1与圆
,且直线PF1与圆
 相切,则该双曲线的渐近线方程为
相切,则该双曲线的渐近线方程为
A. |
B. |
C. |
D. |
来源:2011届湖北省武汉市高三四月调研测试数学文卷
给出下列三种说法:
①“若a>b,则 ”的否命题是假命题;
”的否命题是假命题;
②命题“若m>0,则 有实数根”的逆否命题是真命题;
有实数根”的逆否命题是真命题;
③“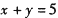 ”是“
”是“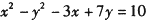 ”的充分非必要条件.
”的充分非必要条件.
其中正确说法的序号是___ ____
____
来源:2011届湖北省武汉市高三四月调研测试数学文卷
(本小题满分12分》
有甲、乙两种味道和颜色都极为相似的名酒各3杯.从中挑出3杯称为一次试验,如果能将甲种酒全部挑出来,算作试验成功一次.某人随机地去挑,求:
(I )试验一次就成功的概率是多少?
(II)恰好在第 三次试验成功的概率是多少?
三次试验成功的概率是多少?
(III)连续试验3次,恰好一次试验成功的概率是多少?
来源:2011届湖北省武汉市高三四月调研测试数学文卷
(本小题满分12分)
在三棱锥P-ABC中, 和
和 是边长为
是边长为 的等边三角形,AB=2,
的等边三角形,AB=2, 0,D分别是AB,PB的中点.
0,D分别是AB,PB的中点.
(I )求证:OD//平面PAC;
(II)求证:平面PAB丄平面ABC
(III) 求三棱锥P-ABC的体积
来源:2011届湖北省武汉市高三四月调研测试数学文卷
 ,则
,则 =
=



 =
=




 的前n项和为
的前n项和为 ,若
,若 ,
, 则
则 =
= ,则
,则 =________
=________ 的焦点F的直线与抛物线交于A、B两点,则
的焦点F的直线与抛物线交于A、B两点,则 =_______
=_______ 的展开式中
的展开式中 的系数是_______
的系数是_______ ,则球的表面积等于_______
,则球的表面积等于_______ (其中
(其中 )的图象关于直线x=
)的图象关于直线x= 对称.
对称. 的值;
的值; 的单调减区间.
的单调减区间. 的首项
的首项
 -1}是等比数列
-1}是等比数列 ;
; }的前n项和Sn.
}的前n项和Sn. 粤公网安备 44130202000953号
粤公网安备 44130202000953号