高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷
已知函数f(x)= 为奇函数,则f(g(-1))=( )
为奇函数,则f(g(-1))=( )
| A.-20 | B.-18 | C.-15 | D.17 |
已知函数f(x)=asin 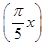 +btan
+btan 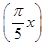 (a,b为常数),若f(1)=1,则不等式f(31)>log2x的解集为________.
(a,b为常数),若f(1)=1,则不等式f(31)>log2x的解集为________.
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知定义在R上的函数y=f(x)满足下列三个条件:①对任意的x∈R都有f(x+2)=-f(x);②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2);③y=f(x+2)的图像关于y轴对称.下列结论中,正确的是( )
| A.f(4.5)<f(6.5)<f(7) |
| B.f(4.5)<f(7)<f(6.5) |
| C.f(7)<f(4.5)<f(6.5) |
| D.f(7)<f(6.5)<f(4.5) |
若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( )
A.(- ,1) ,1) |
B.[- ,1) ,1) |
| C.[-2,1) | D.(-2,1) |
在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,且△ABC,△ACD,△ADB的面积分别为 ,
,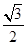 ,
,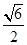 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )
| A.2π | B.6π | C.4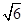 π π |
D.24π |
已知向量α,β,γ满足|α|=1,|α-β|=|β|,(α-γ)·(β-γ)=0.若对每一个确定的β,|γ|的最大值和最小值分别为m,n,则对任意β,m-n的最小值是( )
A. |
B.1 | C.2 | D. |
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设 H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A.a2-2a-16 | B.a2+2a-16 | C.-16 | D.16 |
设函数f(x)=x- ,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.
,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x.若对任意的x∈[a,a+2],不等式f(x+a)≥f2(x)恒成立,则实数a的取值范围是________.
已知数列{an}的前n项和Sn=n2+1,数列{bn}是首项为1,公比为b的等比数列.
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Tn.
已知函数f(x)=ln x-ax(a∈R).
(1)讨论函数f(x)的单调区间;
(2)若函数g(x)= 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围.
 =( )
=( )

 的值域为________.
的值域为________. .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间). 粤公网安备 44130202000953号
粤公网安备 44130202000953号