河南省南阳市高三第三次联考(高考模拟)文科数学试卷
下列命题中正确命题的个数是( )
(1)命题“若 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
(2)设回归直线方程 中,
中, 增加1个单位时,
增加1个单位时, 一定增加2个单位;
一定增加2个单位;
(3)若 为假命题,则
为假命题,则 均为假命题;
均为假命题;
(4)对命题 ,使得
,使得 ,则
,则 ,均有
,均有 ;
;
| A.1 | B.2 | C.3 | D.4 |
已知三棱锥的俯视图与侧视图如图所示,俯视图是变长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知抛物线 的准线与双曲线
的准线与双曲线 两条渐近线分别交于A,B两点,且
两条渐近线分别交于A,B两点,且 ,则双曲线的离心率e为( )
,则双曲线的离心率e为( )
| A.2 | B. |
C. |
D. |
已知 的重心为G,内角A,B,C的对边分别为a,b,c,若
的重心为G,内角A,B,C的对边分别为a,b,c,若 ,则角A为( )
,则角A为( )
A. |
B. |
C. |
D. |
动圆C经过点 ,并且与直线
,并且与直线 相切,若动圆C与直线
相切,若动圆C与直线 总有公共点,则圆C的面积( )
总有公共点,则圆C的面积( )
A.有最大值 |
B.有最小值 |
C.有最小值 |
D.有最小值 |
在等差数列 中,
中, ,其前n项和为
,其前n项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为q,且
,公比为q,且 ,
, .
.
(1)求 与
与 ;
;
(2)设数列 满足
满足 ,求
,求 的前n项和
的前n项和 .
.
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
如图所示,ABCD是正方形, 平面ABCD,E,F是AC,PC的中点.
平面ABCD,E,F是AC,PC的中点.
(1)求证: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
已知圆 ,直线
,直线 与圆
与圆 相切,且交椭圆
相切,且交椭圆 于
于 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距, .
.
(1)求m的值;
(2)O为坐标原点,若 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的条件下,设椭圆 的左右顶点分别为A,B,动点
的左右顶点分别为A,B,动点 ,直线
,直线 与直线
与直线 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.
已知函数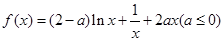 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)当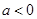 时,讨论
时,讨论 的单调性;
的单调性;
(3)若对任意的 ,
, ,恒有
,恒有 成立,求实数
成立,求实数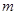 的取值范围.
的取值范围.
如图,直线AB过圆心O,交 于F(不与B重合),直线
于F(不与B重合),直线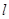 与
与 相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
求证:(1) ;(2)
;(2) .
.
已知曲线C的极坐标方程为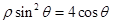 ,直线
,直线 的参数方程为
的参数方程为 (t为参数,
(t为参数, ).
).
(1)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(2)若直线 经过点
经过点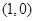 ,求直线
,求直线 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
 是实数集
是实数集 ,集合
,集合 ,
, ,则
,则 为( )
为( )



 满足
满足 (
( 为虚数单位),则
为虚数单位),则 中,如果
中,如果 ,
, ,则数列
,则数列




 的图像在
的图像在 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则 的取值范围是( )
的取值范围是( )



 且
且 ,则下面结论正确的是( )
,则下面结论正确的是( )



 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )



 ,若目标函数
,若目标函数 (
( )的最大值为8,则
)的最大值为8,则 的最小值为 .
的最小值为 . ,
, ,
, ,则
,则 的大小关系是 .
的大小关系是 . 在直线
在直线 上,则
上,则 的值等于 .
的值等于 . 中,
中, ,
, ,
, ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是 .
都在同一球面上,则该球的表面积是 . .
. 时,
时, ,求a的取值范围;
,求a的取值范围; ,
, 恒成立,求实数a的最小值.
恒成立,求实数a的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号