[湖北]2014届湖北省鄂州市九年级上学期期末考试数学试卷
在平面直角坐标系中,点A(1,3)关于原点O对称的点A′的坐标为( )
| A.(-1,3) | B.(1,-3) | C.(3,1) | D.(-1,-3) |
下列函数中,当x>0时,y的值随x的值增大而增大的是( )
| A.y=-x2 | B.y=x-1 | C.y=-x+1 | D.y= |
商场举行摸奖促销活动,对于“抽到一等奖的概率为0.1”,下列说法正确的是( )
| A.抽10次必有一次抽到一等奖 |
| B.抽一次不可能抽到一等奖 |
| C.抽10次也可能没有抽到一等奖 |
| D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖 |
若式子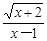 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
| A.x≥-2 | B.x>-2且x≠1 |
| C.x≤-2 | D.x≥-2且x≠1 |
将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
A. |
B. |
C. |
D.3 |
如图,直线AB、AD分别与⊙O相切于点B、D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )
A.70° B.105° C.100° D.110°
如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B.6cm C.7cm D.8cm
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0;则正确的结论是( )
| A.①②③④ | B.②④⑤ | C.②③④ | D.①④⑤ |
某校准备组织师生观看北京奥运会球类比赛,在不同时间段里有3场比赛,其中2场是乒乓球赛,1场是羽毛球赛,从中任意选看2场,则选看的2场恰好都是乒乓球比赛的概率是 .
如图,直线 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
如图,在平面直角坐标系中,抛物线y= 经过平移得到抛物线y=
经过平移得到抛物线y= ,其对称轴与两段抛物线所围成的阴影部分的面积为 .
,其对称轴与两段抛物线所围成的阴影部分的面积为 .
已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1,x2.
⑴求k的取值范围;
⑵若|x1+x2|=x1x2-1,求k的值.
如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,AF⊥DF于F,△BEA旋转后能与△DFA重叠.
⑴△BEA绕_______点________时针方向旋转_______度能与△DFA重合;
⑵若AE= cm,求四边形AECF的面积.
cm,求四边形AECF的面积.
为丰富学生的学习生活,某校九年级1班组织学生参加春游活动,所联系的旅行社收费标准如下:
|
|

已知甲同学手中藏有三张分别标有数字 ,
, ,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片的外形相同,现从甲、乙两人手中各任取一张卡片,并将它们的数字分别记为a、b.
,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片的外形相同,现从甲、乙两人手中各任取一张卡片,并将它们的数字分别记为a、b.
⑴请你用树形图或列表法列出所有可能的结果;
⑵现制订这样一个游戏规则,若所选出的a、b能使ax2+bx+1=0有两个不相等的实数根,则称甲胜;否则乙胜,请问这样的游戏规则公平吗?请你用概率知识解释.
如图,AB为⊙O的直径,AD与⊙O相切于一点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
⑴求证:BC为⊙O的切线;
⑵若 ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例,在营销过程中得到了表格中的数据,
| 薄板的边长(cm) |
20 |
30 |
| 出厂价(元/张) |
50 |
70 |
⑴求一张薄板的出厂价与边长之间满足的函数关系式;
⑵已知出厂一张边长为40cm的薄板,获得利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长这之间满足的函数关系式.
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
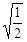
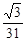
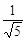
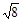
 是方程
是方程 的两根,则
的两根,则 的值为
的值为

 .
. ,则△ABC的周长是 .
,则△ABC的周长是 .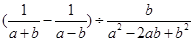 ,其中a=1-
,其中a=1-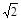 ,b=1+
,b=1+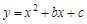 的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。
的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。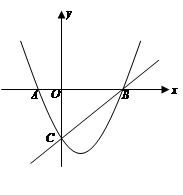
 粤公网安备 44130202000953号
粤公网安备 44130202000953号