山东省青岛市高三第一次模拟考试数学理卷
已知直线 、
、 ,平面
,平面 、
、 ,且
,且 ,
, ,则
,则 是
是 的 ( )
的 ( ) .充要条件
.充要条件  .充分不必要条件
.充分不必要条件 .必要不充分条件
.必要不充分条件  .既不充分也不必要条件
.既不充分也不必要条件
下图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为 和
和 ,腰长为
,腰长为 的等腰梯形,则该几何体的体积是 ( )
的等腰梯形,则该几何体的体积是 ( )
 .
.
 .
.
 .
.
 .
.
.下列四个命题中,正确的是 ( ) .已知函数
.已知函数 ,则
,则 ;
; .设回归直线方程为
.设回归直线方程为 ,当变量
,当变量 增加一个单位时,
增加一个单位时, 平均增加
平均增加 个单位;
个单位; .已知
.已知 服从正态分布
服从正态分布 ,
, ,且
,且 ,则
,则
 .对于命题
.对于命题 :
: ,使得
,使得 ,则
,则 :
: ,均有
,均有
(本小题满分12分)
已知向量 ,
, ,向量
,向量 ,
, ,函数
,函数 .
.
(Ⅰ)求 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知 ,
, ,
, 分别为
分别为 内角
内角 ,
, ,
, 的对边,
的对边, 为锐角,
为锐角, ,
, ,且
,且 恰是
恰是 在
在 ,
, 上的最大值,求
上的最大值,求 ,
, 和
和 的面积
的面积 .
.
(本小题满分12分)
如图, 为矩形,
为矩形, 为梯形,平面
为梯形,平面
 平面
平面 ,
, ,
, ,
, .
.
(Ⅰ)若 为
为 中点,求证:
中点,求证: 平面
平面 ;
;
(Ⅱ)求平面 与
与 所成锐二面角的余弦值.
所成锐二面角的余弦值.
.(本小题满分12分)
某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
| 休假次数 |
 |
 |
 |
 |
| 人数 |
 |
 |
 |
 |
根据上表信息解答以下问题:
(Ⅰ)从该单位任选两名职工,用 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数 在区间
在区间 ,
, 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 发生的概率
发生的概率 ;
;
(Ⅱ)从该单位任选两名职工,用 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分12分)
已知数列 满足
满足 ,且
,且 ,
, 为
为 的前
的前 项和.
项和.
(Ⅰ)求证:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(Ⅱ)如果对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 ,
, 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令 ,若
,若 在
在 ,
, 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
 ,则复数
,则复数 的共轭复数为 ( )
的共轭复数为 ( ) .
.
 .
.
 .
.
 .
.
 ,集合
,集合 ,
, ,则
,则 等于
等于 .
.
 .
.
 .
.
 .
.
 ,
, 上是减函数的是 ( )
上是减函数的是 ( ) .
.
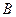 .
.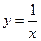
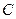 .
.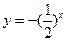
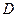 .
.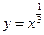
 的展开式中,
的展开式中, 项的系数为 ( )
项的系数为 ( ) .
.
 .
.
 .
.
 .
.
 圆心的抛物线方程是
圆心的抛物线方程是 .
.
 .
.
 .
.
 .
.
 ,若
,若 的最大值为
的最大值为 ,则
,则 的值是( )
的值是( ) .
.
 .
.
 .
. .
.
 的前项和为
的前项和为 ,若
,若 、
、 、
、 三点共线,
三点共线, 为坐标原点,且
为坐标原点,且 (直线
(直线 不过点
不过点 等于 ( )
等于 ( ) .
.
 .
.
 .
.
 .
.
 ,将函数
,将函数 向左平移
向左平移 个单位
个单位 ,所得图象对应的函数为偶函数,则
,所得图象对应的函数为偶函数,则 .
.
 .
.
 .
.
 .
.
 ,当
,当 ,
, 时,
时, ,若在区间
,若在区间 ,
, 有两个零点,则实数
有两个零点,则实数 的取值范围是 ( )
的取值范围是 ( ) .
. ,
,
 .
. ,
,
 .
.
 .
. ,
,
 辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过
辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过 的汽车数量为
的汽车数量为 
 的值为
的值为 ,图中判断框内
,图中判断框内 处应填的数为
处应填的数为 
 对一切非零实数
对一切非零实数 恒成立,则实数
恒成立,则实数 的取值范围
的取值范围  是曲线
是曲线 上任意一点,则点
上任意一点,则点 的距离的最小值是
的距离的最小值是  :
: ,点
,点 ,
, ,点
,点 在圆
在圆 的垂直平分线交
的垂直平分线交 于点
于点 .
. 的方程;
的方程; 分别是曲线
分别是曲线 在第一象限,点
在第一象限,点 在第三象限,若
在第三象限,若 ,
, 为坐标原点,求直线
为坐标原点,求直线 的斜率
的斜率 ;
; ,
, 且斜率为
且斜率为 交曲线
交曲线 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号