[安徽]2014届安徽省“皖西七校”高三年级联合考试理科数学试卷
复数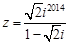 (
( 是虚数单位)在复平面内的对应点位于( )
是虚数单位)在复平面内的对应点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
命题“若 ,则一元二次方程
,则一元二次方程 有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
| A.0 | B.2 | C.4 | D.不确定 |
一个几何体按比例绘制的三视图如右图所示(单位: ),则该几何体的体积为( )
),则该几何体的体积为( )

A. |
B. |
C. |
D. |
已知 是两个不同的平面,下列四个条件中能推出
是两个不同的平面,下列四个条件中能推出 的是( )
的是( )
①存在一条直线 ; ②存在一个平面
; ②存在一个平面 ;
;
③存在两条平行直线 ;
;
④存在两条异面直线 .
.
| A.①③ | B.②④ | C.①④ | D.②③ |
设定义在 上的函数
上的函数 是最小正周期为
是最小正周期为 的偶函数,
的偶函数, 是
是 的导函数,当
的导函数,当 时;
时; ;当
;当 且
且 时,
时, ,则函数
,则函数 在区间
在区间 上的零点个数为( )
上的零点个数为( )
| A.2 | B.4 | C.6 | D.8 |
设函数 ,若对任意给定的
,若对任意给定的 ,都存在唯一的
,都存在唯一的 ,满足
,满足 ,则正实数
,则正实数 的最小值是( )
的最小值是( )
A. |
B. |
C.2 | D.4 |
方程 的曲线即为函数
的曲线即为函数 的图象,对于函数
的图象,对于函数 ,下列命题中正确的是 .(请写出所有正确命题的序号)
,下列命题中正确的是 .(请写出所有正确命题的序号)
①函数 在
在 上是单调递减函数; ②函数
上是单调递减函数; ②函数 的值域是
的值域是 ;
;
③函数 的图象不经过第一象限; ④函数
的图象不经过第一象限; ④函数 的图象关于直线
的图象关于直线 对称;
对称;
⑤函数 至少存在一个零点.
至少存在一个零点.
已知函数 的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在
的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在 中,角
中,角 对边为
对边为 ,
, ,且满足
,且满足 .
.
(Ⅰ)求 的面积;
的面积;
(Ⅱ)求函数 的单调递增区间.
的单调递增区间.
如图1,已知 的直径
的直径 ,点
,点 、
、 为
为 上两点,且
上两点,且 ,
, ,
, 为弧
为弧 的中点.将
的中点.将 沿直径
沿直径 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).
(Ⅰ)求证: ;
;
(Ⅱ)在弧 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,试指出点
?若存在,试指出点 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(Ⅲ)求二面角 的正弦值.
的正弦值.
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(Ⅰ)求水面宽;
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
在平面直角坐标系中,已知点 和
和 ,圆
,圆 是以
是以 为圆心,半径为
为圆心,半径为 的圆,点
的圆,点 是圆
是圆 上任意一点,线段
上任意一点,线段 的垂直平分线
的垂直平分线 和半径
和半径 所在的直线交于点
所在的直线交于点 .
.
(Ⅰ)当点 在圆上运动时,求点
在圆上运动时,求点 的轨迹方程
的轨迹方程 ;
;
(Ⅱ)已知 ,
, 是曲线
是曲线 上的两点,若曲线
上的两点,若曲线 上存在点
上存在点 ,满足
,满足 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
 ,且
,且 与
与 的夹角为
的夹角为 ,当
,当 取得最小值时,实数
取得最小值时,实数 的值为( )
的值为( )

 ,集合
,集合 ,则
,则 ( )
( )



 是等差数列,
是等差数列, ,设
,设 为数列
为数列 的前
的前 项和,则
项和,则 ( )
( )

 ,两动点
,两动点 在双曲线
在双曲线 的右支上,则
的右支上,则 的最小值是( )
的最小值是( )



 ,则
,则 .
. (
( 且
且 )的图象恒过定点
)的图象恒过定点 ,则不等式组
,则不等式组 所表示的平面区域的面积是 .
所表示的平面区域的面积是 . ,且
,且 ,则
,则 的最小值是 .
的最小值是 . 中,
中, ,
, ,
, ,则
,则 与平面
与平面 所成角的余弦值为 .
所成角的余弦值为 . ,其中
,其中 .
. ,求函数
,求函数 的极值点;
的极值点; 内单调递增,求实数
内单调递增,求实数 的取值范围.
的取值范围. 的前
的前 项和为
项和为 满足
满足 .
. 与函数
与函数 互为反函数,令
互为反函数,令 ,求数列
,求数列 的前
的前 ;
; 满足
满足 ,证明:对任意的整数
,证明:对任意的整数 ,有
,有 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号