[河南]2014届河南省中原名校高三上学期期中联考理科数学试卷
若集A={x|-1≤2x+1≤3},B={x| ≤0},则A∪B=( )
≤0},则A∪B=( )
| A.{x|-1≤x<2} | B.{x|-1≤x≤2} |
| C.{x|0≤x≤2} | D.{x|0≤x≤1} |
设f(x)=lgx+x-3,用二分法求方程lgx+x-3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
| A.(2,2.25) | B.(2.25,2.5) |
| C.(2.5,2.75) | D.(2.75,3) |
已知α,β为不重合的两个平面,直线m α,那么“m⊥β”是“α⊥β”的( )
α,那么“m⊥β”是“α⊥β”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
函数f(x)=Asin(ωx+ )(其中A>0,ω>0,|
)(其中A>0,ω>0,| |<
|< )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
A.向右平移 个长度单位 个长度单位 |
B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
已知{ }为等差数列,其公差为-2,且a7是a3与a9的等比中项,
}为等差数列,其公差为-2,且a7是a3与a9的等比中项, 为{
为{ }的前n项和,n∈N﹡,则S10的值为( )
}的前n项和,n∈N﹡,则S10的值为( )
| A.-110 | B.-90 | C.90 | D.110 |
已知x>0,y>0,若 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
| A.m≥4或m≤-2 | B.m≥2或m≤-4 |
| C.-2<m<4 | D.-4<m<2 |
已知向量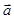 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量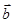 =(
=(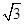 ,-1),则|2
,-1),则|2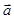 -
-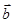 |的最大值与最小值的和是( )
|的最大值与最小值的和是( )
A.4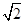 |
B.6 | C.4 | D.16 |
已知函数f(x)= +
+ +
+ +…+
+…+ +
+ (n>2且n∈N﹡)设
(n>2且n∈N﹡)设 是函数f(x)的零点的最大值,则下述论断一定错误的是( )
是函数f(x)的零点的最大值,则下述论断一定错误的是( )
A. |
B. =0 =0 |
C. >0 >0 |
D. <0 <0 |
给出下列四个命题:
①命题p: ∈R,sinx≤1,则
∈R,sinx≤1,则 :
: ∈R,sinx<1.
∈R,sinx<1.
②当a≥1时,不等式|x-4|+|x-3|<a的解集为非空.
③当x>0时,有lnx+ ≥2.
≥2.
④设复数z满足(1-i)z=2i,则z=1-i.
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知F是双曲线 (a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
A.(1,+∞) B.(1,2) C.(1,1+ ) D.(2,1+
) D.(2,1+ )
)
已知 =
= ,把数列{
,把数列{ }的各项排列成如下的三角形状,
}的各项排列成如下的三角形状,
记A(m,n)表示第m行的第n个数,则A(10,12)=( )
A. |
B. |
C. |
D. |
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=a (a>0).使得
(a>0).使得 =λ·(
=λ·( +
+ )(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
)(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
| A.(2,+∞) | B.(3,+∞) | C.[4,+∞) | D.[8,+∞) |
在平面直角坐标系中,记抛物线y=x- 与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为A,向区域M内随机抛掷一点P,若点P落在区域A内的概率为
与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为A,向区域M内随机抛掷一点P,若点P落在区域A内的概率为 ,则k的值为__________.
,则k的值为__________.
如图,在四边形ABCD中, =λ
=λ (λ∈R),|
(λ∈R),| |=|
|=| |=2,|
|=2,| -
- |=2
|=2 ,且△BCD是以BC为斜边的直角三角形,则
,且△BCD是以BC为斜边的直角三角形,则 ·
· 的值为__________.
的值为__________.

已知各项均为正数的数列{ }满足
}满足 -
- -2
-2 =0,n∈N﹡,且
=0,n∈N﹡,且 是a2,a4的等差中项.
是a2,a4的等差中项.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若 =
=
 ,
, =b1+b2+…+
=b1+b2+…+ ,求
,求 的值.
的值.
在△ABC中,A、B、C为三个内角,a、b、c为相应的三条边, <C<
<C< ,且
,且 =
= .
.
(1)判断△ABC的形状;
(2)若| +
+ |=2,求
|=2,求 ·
· 的取值范围.
的取值范围.
已知函数f(x)= -(a+2)x+lnx.
-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e)上的最小值为-2,求a的取值范围.
已知A(-5,0),B(5,0),动点P满足| |,
|, |
| |,8成等差数列.
|,8成等差数列.
(1)求P点的轨迹方程;
(2)对于x轴上的点M,若满足| |·|
|·| |=
|= ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
 的展开式中常数项为___________________.
的展开式中常数项为___________________. ,若z的最大值为6,则z的最小值为_________.
,若z的最大值为6,则z的最小值为_________. ,tan(α-β)=-
,tan(α-β)=- .求cosβ的值.
.求cosβ的值.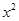 +
+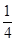 ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数)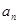 }中,a1=1,
}中,a1=1,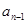 )(n≥2),求证:
)(n≥2),求证: <
<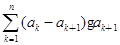 <
<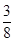 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号