[天津]2014届天津市高三第一次六校联考文科数学试卷
“ ”是“
”是“ ” 的( )
” 的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2014届天津市高三第一次六校联考文科数学试卷
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5 杯,其颜色完全相同,并且其中3杯为 饮料,另外2杯为
饮料,另外2杯为 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯 饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对
饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对 和
和 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;
(Ⅱ)求此人被评为良好及以上的概率.
来源:2014届天津市高三第一次六校联考文科数学试卷
在三棱拄 中,
中, 侧面
侧面 ,已知
,已知 ,
, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)试在棱 (不包含端点
(不包含端点 )上确定一点
)上确定一点 的位置,使得
的位置,使得 ;
;
(Ⅲ)在(Ⅱ)的条件下,求 和平面
和平面 所成角正弦值的大小.
所成角正弦值的大小.
来源:2014届天津市高三第一次六校联考文科数学试卷
在直角坐标系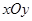 中,点
中,点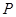 到两点
到两点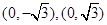 的距离之和等于4,设点
的距离之和等于4,设点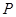 的轨迹为
的轨迹为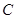 ,直线
,直线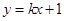 与
与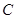 交于
交于 两点.
两点.
(1)写出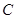 的方程;
的方程;
(2)  ,求
,求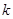 的值.
的值.
来源:2014届天津市高三第一次六校联考文科数学试卷
已知正项数列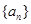 的前
的前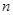 项和为
项和为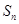 ,
,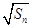 是
是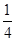 与
与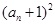 的等比中项.
的等比中项.
(1)求证:数列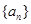 是等差数列;
是等差数列;
(2)若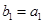 ,且
,且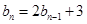 ,求数列
,求数列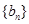 的通项公式;
的通项公式;
(3)在(2)的条件下,若 ,求数列
,求数列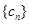 的前
的前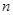 项和
项和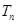 .
.
来源:2014届天津市高三第一次六校联考文科数学试卷
 ,那么
,那么 =( )
=( )



 满足
满足 ,则目标函数
,则目标函数 的最大值和最小值分别为( )
的最大值和最小值分别为( )

 的根所在区间为( )
的根所在区间为( )



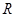 上的函数
上的函数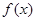 是偶函数,对
是偶函数,对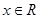 都有
都有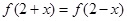 ,当
,当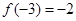 时,
时,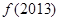 的值为( )
的值为( )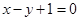 与圆
与圆 有公共点,则实数
有公共点,则实数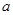 取值范围是( )
取值范围是( )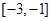
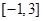
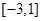
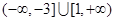
 中,
中, ,
, ,
, ,则
,则



 ,则使方程
,则使方程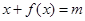 有解的实数
有解的实数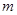 的取值范围是( )
的取值范围是( )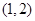
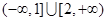
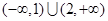
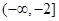
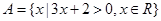 ,
,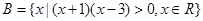 ,则
,则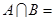 .
.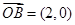 ,
,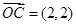 ,
,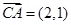 ,则
,则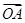 与
与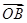 夹角的正弦值为_____.
夹角的正弦值为_____.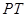 切圆
切圆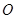 于点
于点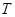 ,
,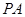 交圆
交圆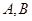 两点,且与直径
两点,且与直径 交于点
交于点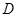 ,
,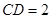 ,
,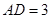 ,
,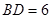 ,则
,则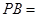 .
. 

 ,
, ,
, ,
, ,则输出的数等于 .
,则输出的数等于 .
 和椭圆
和椭圆 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .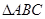 中,角
中,角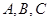 所对的边分别为
所对的边分别为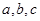 且满足
且满足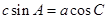 .
.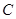 的大小;
的大小;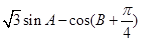 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角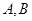 的大小.
的大小.
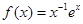 的定义域为
的定义域为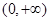 .
.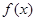 在
在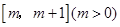 上的最小值;
上的最小值;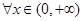 ,不等式
,不等式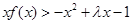 恒成立,求
恒成立,求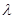 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号