安徽省皖南八校高三第一次联考理科数学卷
命题“对任意直线l,有平面 与其垂直”的否定是 ( )
与其垂直”的否定是 ( )
A.对任意直线l,没有平面 与其垂直 与其垂直 |
B.对任意直线l,没有平面 与其不垂直 与其不垂直 |
C.存在直线 ,有平面 ,有平面 与其不垂直 与其不垂直 |
D.存在直线 ,没有平面 ,没有平面 与其不垂直 与其不垂直 |
设点P是双曲线 与圆
与圆 在第一象限的交点F1,F2分别是双曲线的左、右焦点,且
在第一象限的交点F1,F2分别是双曲线的左、右焦点,且 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A. |
B. |
C. |
D. |
有一种波,其波形为函数 的图象,若在区间
的图象,若在区间 上至少有2个波峰(图象的最高点),则正整数
上至少有2个波峰(图象的最高点),则正整数 的最小值是 ( )
的最小值是 ( )
| A.3 | B.4 |
| C.5 | D.6 |
考察底为等腰直角三角形的直三棱柱的9条棱,甲从这9条棱中任选一条,乙从这9条棱中任选一条,则这两条棱互相垂直的概率为 ( )
A. |
B. |
C. |
D. |
在平面直角坐标系 中,以O为极点,
中,以O为极点, 轴正半轴为极辆,取相同的长度单位,建立极坐标系,则直线
轴正半轴为极辆,取相同的长度单位,建立极坐标系,则直线 被圆
被圆 为参数)截得的弦长为 。
为参数)截得的弦长为 。
一个几何体的三视图及其尺寸如右图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视国科是等腰三角形,则这个几何体的表面积是 cm2。
若定义域为R的奇函数 ,
,
则下列结论:① 的图象关于点
的图象关于点 对称;
对称;
② 的图象关于直线
的图象关于直线 对称;③
对称;③ 是周期函数,且2个它的一个周期;④
是周期函数,且2个它的一个周期;④ 在区间(—1,1)上是单调函数,其中正确结论的序号是 。(填上你认为所有正确结论的序号)
在区间(—1,1)上是单调函数,其中正确结论的序号是 。(填上你认为所有正确结论的序号)
(本小题满分12分)
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码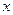 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码 ,设随机变量
,设随机变量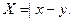
(1)求 的概率;
的概率;
(2)求随机变量X的分布列及数学期望。
(本小题满分12分)
在如图所示的空间几何体中,平面 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在 的平分线上。
的平分线上。
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积。
(本小题满分13分)
在数列 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,求数列
,求数列 的前
的前 项和。
项和。
(本小题满分13分)
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线, 交E于A,B两点,
交E于A,B两点, 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求 k的取值范围;
k的取值范围;
(3)求 的取值范围。
的取值范围。
 ,则
,则 等于 ( )
等于 ( )



 等于 ( )
等于 ( ) 



 则q等于
则q等于 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( ) ,则输入框应填入
,则输入框应填入




 上不是单调函数,则函数
上不是单调函数,则函数 在区间
在区间 上的图象可能是 ( )
上的图象可能是 ( )
 = 。
= 。 的展开式中,各项的系数和比各项的二项系数和大240,则
的展开式中,各项的系数和比各项的二项系数和大240,则 的值为 。
的值为 。 ,角A,B,C的对边分别为
,角A,B,C的对边分别为 。
。 的值。
的值。 为自然对数的底数)
为自然对数的底数) 的单调区间,若
的单调区间,若 有最值,请求出最值;
有最值,请求出最值; ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号