[山西]2014届山西省高三第一次四校联考文数学卷
袋中共有5个除颜色外完全相同的小球,其中1个红球,2个白球和2个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于( )
A. |
B. |
C. |
D.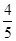 |
来源:2014届山西省高三第一次四校联考文数学卷
阅读如图所示程序框图,运行相应的程序,若输入 1则输出的结果为 ( )
1则输出的结果为 ( )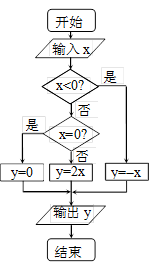
| A.-1 | B.2 | C.0 | D.无法判断 |
来源:2014届山西省高三第一次四校联考文数学卷
过抛物线 的焦点F作一直线l交抛物线于A、B两点,以AB为直径的圆与该抛物线的准线l的位置关系为( )
的焦点F作一直线l交抛物线于A、B两点,以AB为直径的圆与该抛物线的准线l的位置关系为( )
A. 相交 B. 相离 C. 相切 D. 不能确定
来源:2014届山西省高三第一次四校联考文数学卷
下面有四个命题:
①函数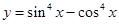 的最小正周期是
的最小正周期是 ;
;
②函数 的最大值是5;
的最大值是5;
③把函数 的图象向右平移
的图象向右平移 得
得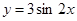 的图象;
的图象;
④函数 在
在 上是减函数.
上是减函数.
其中真命题的序号是 .
来源:2014届山西省高三第一次四校联考文数学卷
为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”
(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?
(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:
表1
| 数学成绩 |
90分以下 |
90—120分 |
120—140分 |
140分以上 |
| 频 数 |
15 |
20 |
10 |
5 |
表2
| 数学成绩 |
90分以下 |
90—120分 |
120—140分 |
140分以上 |
| 频 数 |
5 |
40 |
3 |
2 |
完成下面2×2列联表,并回答是否有99%的把握认为这两种教学法有差异.
| 班 次 |
120分以下(人数) |
120分以上(人数) |
合计(人数) |
| 一班 |
|
|
|
| 二班 |
|
|
|
| 合计 |
|
|
|
参考公式: ,其中
,其中
参考数据:
| P(K2≥k0) |
0.40 |
0.25 |
0.10 |
0.05 |
0.010 |
0.005 |
| k0 |
0.708 |
1.323 |
2.706 |
3.841 |
6.635 |
7.879 |
来源:2014届山西省高三第一次四校联考文数学卷
设椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,过点
,过点 且与
且与 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 .
.
(1) 求椭圆方程.
(2) 过点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,当
,当 面积最大时,求
面积最大时,求 .
.
来源:2014届山西省高三第一次四校联考文数学卷
在平面直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,过点
,过点 (-2,-4)的直线
(-2,-4)的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 与曲线
与曲线 相交于
相交于 两点.
两点.
(Ⅰ)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(Ⅱ)若 ,求
,求 的值.
的值.
来源:2014届山西省高三第一次四校联考文数学卷
 ,则
,则
 ( )
( )



 是虚数单位,则满足
是虚数单位,则满足 的复数
的复数 为( )
为( )



 的离心率
的离心率 ,则它的渐近线方程为 ( )
,则它的渐近线方程为 ( )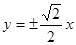






 ,使得
,使得 ,命题q:
,命题q: 
 .则下列命题中真命题为( )
.则下列命题中真命题为( )



 的零点所在的区间为( )
的零点所在的区间为( )



 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 =( )
=( )
 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、 ,已知
,已知 ,
, B.
B. C.
C. D.
D.
 ,若
,若 ,则实数
,则实数 的取值范围为( )
的取值范围为( )



 ,
, 满足
满足 ,
, ,
, ,则向量
,则向量 ,
, 满足
满足 则变量
则变量 的最小值为 .
的最小值为 . 的侧棱
的侧棱 两两垂直且长度分别为2cm,2cm,1cm,则其
两两垂直且长度分别为2cm,2cm,1cm,则其 为其前n项和
为其前n项和 ,且
,且
 ,求数列
,求数列 的前
的前 项和
项和 .
. 中,
中, ,
, ,
,  ,
, ,
, ,
, .
.
 ∥
∥ ;
; 求四棱锥
求四棱锥 的体积
的体积 (
( R),且该函数曲线
R),且该函数曲线 在
在 处的切线与
处的切线与 轴平行.
轴平行. 的单调性;
的单调性; 时,
时, .
. 为圆
为圆 的切线,切点为
的切线,切点为 ,直径
,直径 ,连接
,连接 交
交 于点
于点 .
.
 ;
; .
. .
.
 成立的
成立的 的取值范围;
的取值范围; ,
, ,求实数
,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号