[甘肃]2013年初中毕业升学考试(甘肃天水卷)数学
下列计算正确的是【 】
| A.a3+a2=2a5 | B.(﹣2a3)2=4a6 | C.(a+b)2=a2+b2 | D.a6÷a2=a3 |
函数y1=x和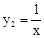 的图象如图所示,则y1>y2的x取值范围是
的图象如图所示,则y1>y2的x取值范围是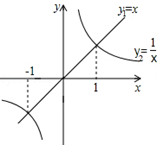
| A.x<﹣1或x>1 | B.x<﹣1或0<x<1 |
| C.﹣1<x<0或x>1 | D.﹣1<x<0或0<x<1 |
一个三角形的两边长分别为3和6,第三边的边长是方程(x﹣2)(x﹣4)=0的根,则这个三角形的周长是【 】
| A.11 | B.11或13 | C.13 | D.以上选项都不正确 |
一组数据:3,2,1,2,2的众数,中位数,方差分别是【 】
| A.2,1,0.4 | B.2,2,0.4 | C.3,1,2 | D.2,1,0.2 |
从一块正方形的木板上锯掉2m宽的长方形木条,剩下的面积是48m2,则原来这块木板的面积是【 】
| A.100m2 | B.64m2 | C.121m2 | D.144m2 |
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于【 】
| A.3 | B.﹣3 | C. |
D. |
如图,已知等边三角形ABC的边长为2,E、F、G分别是边AB、BC、CA的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y与x的函数图象大致是【 】
A. B.
B. C.
C. D.
D.
如图所示,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=5,则这个梯形中位线的长等于 .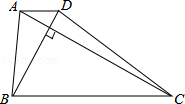
有两块面积相同的小麦试验田,分别收获小麦9000kg和15000kg.已知第一块试验田每公顷的产量比第二块少3000kg,若设第一块试验田每公顷的产量为xkg,根据题意,可得方程 .
已知⊙O1的半径为3,⊙O2的半径为r,⊙O1与⊙O2只能画出两条不同的公共切线,且O1O2=5,则⊙O2的半径为r的取值范围是 .
如图所示,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积是 .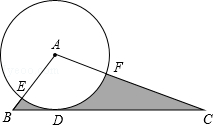
观察下列运算过程:S=1+3+32+33+…+32012+32013 ①,
①×3得3S=3+32+33+…+32013+32014 ②,
②﹣①得2S=32014﹣1,S=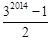 .
.
运用上面计算方法计算:1+5+52+53+…+52013= .
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=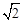 ,BE=
,BE=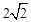 .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.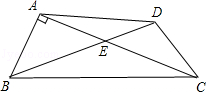
某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况,八年级300名同学零花钱的最主要用途情况,九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.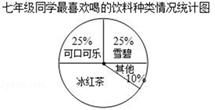
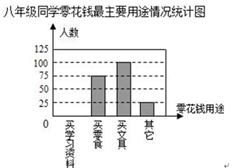
| 时间 |
1小时左右 |
1.5小时左右 |
2小时左右 |
2.5小时左右 |
| 人数 |
50 |
80 |
120 |
50 |
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
如图所示,在天水至宝鸡(天宝)高速公路建设中需要确定某条隧道AB的长度,已知在离地面2700米高度C处的飞机上,测量人员测得正前方AB两点处的俯角分别是60°和30°,求隧道AB的长.(结果保留根号)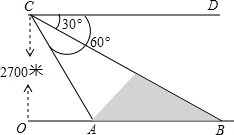
如图在平面直角坐标系xOy中,函数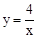 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).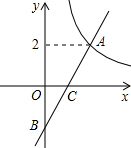
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
| 型号 |
A |
B |
| 成本(万元/台) |
200 |
240 |
| 售价(万元/台) |
250 |
300 |
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价﹣成本)
如图1,已知抛物线
经过
、
两点.
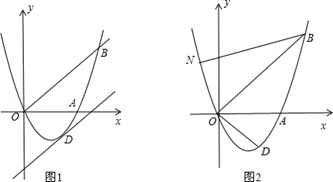
(1)求抛物线的解析式;
(2)将直线
向下平移
个单位长度后,得到的直线与抛物线只有一个公共点
,求
的值及点
的坐标;
(3)如图2,若点
在抛物线上,且
,则在(2)的条件下,求出所有满足
的点
坐标(点
、
、
分别与点
、
、
对应).


 的值为零,那么x的值是 .
的值为零,那么x的值是 .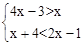 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. .
.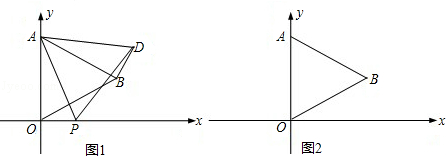
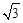 ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;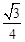 ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号