河南省周口市初一下学期第九章一元一次不等式组检测题
已知:如图,抛物线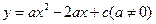 与
与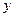 轴交于点
轴交于点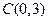 ,与
,与 轴交于
轴交于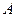 、
、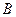 两点,点
两点,点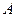 的坐标为
的坐标为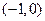 .
.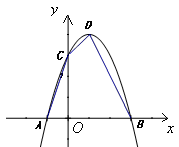
(1)求抛物线的解析式及顶点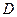 的坐标;
的坐标;
(2)设点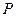 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形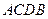 面积相等的四边形
面积相等的四边形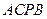 的点
的点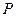 的坐标;
的坐标;
(3)求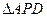 的面积.
的面积.
在边长为4m的正方形中间挖去一个长为xm的小正方 形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________
形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________
用一根长为8m的 木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系
木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系 式为________.
式为________.
下列结论正确的是( )
| A.二次函数中两个变量的值是非零实数; | B.二次函数中变量x的值是所有实数; |
| C.形如y=ax2+bx+c的函数叫二次函数; | D.二次函数y=ax2+bx+c中a,b,c的值均不能为零 |
下列函数中,不是二次函数的是( )
A.y=1- x2 x2 |
B.y=2(x-1)2+4; |
C.y= (x-1)(x+4) (x-1)(x+4) |
D.y=(x-2)2-x2 |
.在半径为4cm 的圆中, 挖去一个半径为xcm 的圆面,剩下一个圆环的面积为ycm2,则y与x的函数关系式为( )
| A.y=πx2-4 | B.y=π(2-x)2; | C.y=-(x2+4) | D.y=-πx2+16π |
若y=(2-m) 是二次函数,则m等于( )
是二次函数,则m等于( )
| A.±2 | B.2 | C.-2 | D.不能确定 |
分别说出下列函数的名称:
(1)y=2x-1 (2)y=-3x2, (3)y= (4)y=3x-x2 (5)y=x
、分别说出下列二次函数的二次项系数、一次项系数和常数项:
(1)d=n2-n, (2)y=1-x2, (3)y=-x(x-3)
二次函数y=ax2+c中,当x=3时,y="26" ;当x=2时,y="11" ;则当x=5时,
y= __ .
、已知一个直角三角形的两条直角边的和为10cm。
(1)求这个直角三角形的面积S与其中一条直角边长x之间的函数关系式和自变量x的取值范围;
(2)求当x=5cm时直角三角形的面积。
、函数y="ax2+bx+c" (a、b、c是常数),问当a、b、c满足什么条件时,
(1)它是二次函数?
(2)它是一次函数?
(3)它是正比例函数?
一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表:
| 时间t(秒) |
1 |
2 |
3 |
4 |
… |
| 距离s(米) |
2 |
8 |
18 |
32 |
… |
写出用t表示s的函数关系式。
、已知y与x2成正比例,并且当x=1时,y=2,求函数y与x的函数关系式,并求当x=-3时,y的值.当y=8时,求x的值.
富根老伯想利用一边长为a米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形。
如果设猪舍的宽AB为x米,则猪舍的总面积S(米2)与x有怎样的函数关系?
请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC和宽AB的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响? 
下列图形不一定相似的是( ).
| A.有一个角是120°的两个等腰三角形; | B.有一个角是60°的两个等腰三角形 |
| C.两个等腰直角三角形; | D.有一个角是45°的两个等腰三角形 |
.如图1,已知△ABC,D,E分别是AB,AC边上的点.AD=3cm,AB=8cm,AC=10cm.若△ADE∽△ABC,则AE的值为( ).
A.
满足下列条件的各对三角形中相似的两个三角形有( ).
| A.∠A=60°,AB=5cm,AC=10cm;∠A′=60°,A′B′=3cm,A′C′=10cm |
| B.∠A=45°,AB=4cm,BC=6cm;∠D=45°,DE=2cm,DF=3cm |
| C.∠C=∠E=30°,AB=8cm,BC=4cm;DF=6cm,FE=3cm |
| D.∠A=∠A′,且AB·A′C′=AC·A′B′ |
如图2,点D为△ABC的AB边一点(AB>AC),下列条件不一定能保证△ACD∽△ABC的是
A.∠ADC=∠ACB B.∠ACD=∠B C.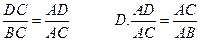

如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积为 ( -)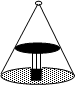
A.0.36 米2 米2 |
B.0.81 米2 米2 |
C.2 米2 米2 |
D.3.24 米2 米2 |
.已知三角形的三条边 长分别为1,
长分别为1, ,
, ,请你写出另外三条线段长,使这三条线段构成的三角形与已知三角形相似:________,________,_______.
,请你写出另外三条线段长,使这三条线段构成的三角形与已知三角形相似:________,________,_______.
如图3,若AC2=CD·CB,则△_______∽△_______,∠ADC=________.
若不等式组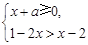 有解,则a的取值范围是( )
有解,则a的取值范围是( )
A.a>-1. B.a≥-1. C a≤1. D.a<1.
不等式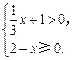 的解集是( )
的解集是( )
A.- <x≤2 <x≤2 |
B.-3<x≤2 | C.x ≥2 ≥2 |
D.x<-3 |
. 如果不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是. ( )
| A.a>0 | B.a<0 | C.a>-1 | D.a<-1 |
若不等式组 的解集为
的解集为 ,则a的取值范围为( )
,则a的取值范围为( )
| A.a>0 | B.a=0 | C.a>4 | D.a=4 |
已知关于x的不等式组 的整数解共有4个,则
的整数解共有4个,则 的最小值为( )
的最小值为( )
| A.2 | B.2.1 | C.3 | D.1 |
(8分)已知不等式:⑴1-x<0;⑵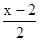 <1;⑶ 2x+3>1;⑷ 0.2x-3<-2.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来
<1;⑶ 2x+3>1;⑷ 0.2x-3<-2.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来
(10分)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
. (10分)今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(10分)今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
(12分)2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和295 0盆乙种花卉搭配
0盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个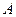 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个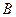 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个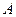 种造型的成本是800元,搭配一个
种造型的成本是800元,搭配一个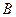 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
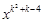 是关于x的二次函数,则k=________
是关于x的二次函数,则k=________
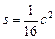
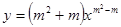 是二次函数,求m的值。
是二次函数,求m的值。
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )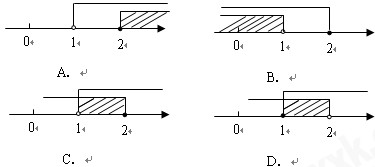
 有解,那么
有解,那么 的取值范围是( )
的取值范围是( )

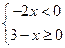 的正整数解的个数是( )
的正整数解的个数是( ) 的解集是( )
的解集是( )







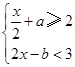 的解集是
的解集是 ,那么
,那么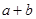 的值为 .
的值为 . 的解集是x<m-2,则m的取值应为_________。
的解集是x<m-2,则m的取值应为_________。 的整数解为
的整数解为  的解集是___________________.
的解集是___________________.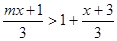 的解集为x >5,则m值为___________
的解集为x >5,则m值为___________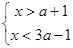 无解,则
无解,则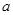 的取值范围是______
的取值范围是______ 的解集是 _____________.
的解集是 _____________.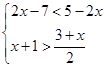 的整数解是 .
的整数解是 .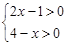 的解集是 。
的解集是 。 的不等式组
的不等式组 的整数解共有5个,则
的整数解共有5个,则 的取值范围是______
的取值范围是______ ,并把解集在数轴上表示出
,并把解集在数轴上表示出 来.
来.

 把解集表示在数轴上,并求出不等式组的整数解.
把解集表示在数轴上,并求出不等式组的整数解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号