[河南]2013届河南省十所名校高三第三次联考文科数学试卷
设全集U是实数集R,集合M={x|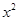 ≥2x},N={x|
≥2x},N={x|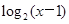 ≤0},则M∩N=( )
≤0},则M∩N=( )
| A.{1,2} | B.{ 2 } | C.{1} | D.[1,2] |
某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )
| A.117 | B.118 | C.118.5 | D.119.5 |
在△ABC中,M是AB边所在直线上任意一点,若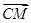 =-2
=-2 +λ
+λ ,则λ=( )
,则λ=( )
| A.1 | B.2 | C.3 | D.4 |
“m=-1”是“函数f(x)=ln(mx)在(-∞,0)上单调递减”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
公差不为0的等差数列{ }的前21项的和等于前8项的和.若
}的前21项的和等于前8项的和.若 ,则k=( )
,则k=( )
| A.20 | B.21 | C.22 | D.23 |
e,π分别是自然对数的底数和圆周率,则下列不等式中不成立的是( )
A.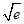 > >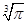 |
B. + + >1 >1 |
C.( ) )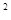 + +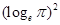 >2 >2 |
D.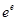 -e> -e>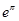 -π -π |
在△ABC中,a,b,c分别是角A,B,C的对边,若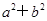 =2014
=2014 ,则
,则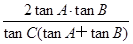 的值为( )
的值为( )
| A.0 | B.1 | C.2013 | D.2014 |
四面体ABCD中,AD与BC互相垂直,且AB+BD=AC+CD.则下列结论中错误的是( )
A.若分别作△BAD和△CAD的边AD上的高,则这两条高所在直线异面
B.若分别作△BAD和△CAD的边AD上的高,则这两条高长度相等
C.AB=AC且DB=DC
D.∠DAB=∠DAC
已知函数f(x)= ,若存在
,若存在 ∈(
∈(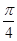 ,
,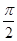 ),使f(sin
),使f(sin )+f(cos
)+f(cos )=0,则实数a的取值范围是_______________.
)=0,则实数a的取值范围是_______________.
设{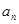 }是等差数列,{
}是等差数列,{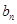 }是等比数列,记{
}是等比数列,记{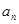 },{
},{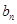 }的前n项和分别为
}的前n项和分别为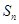 ,
, .若a3=b3,a4=b4,且
.若a3=b3,a4=b4,且 =5,则
=5,则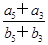 =_____________.
=_____________.
已知函数f(x)=sin2ωx+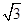 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,
(Ⅰ)求ω的值及函数f(x)的单调增区间;
(Ⅱ)求函数f(x)在[0, ]上的值域.
]上的值域.
一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(Ⅰ)求应从水果类、点心类、小吃类中分别买回的种数;
(Ⅱ)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED是边长为2的正方形,且所在平面垂直于平面ABC.
(Ⅰ)求几何体ABCDFE的体积;
(Ⅱ)证明:平面ADE∥平面BCF;
已知圆C: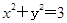 的半径等于椭圆E:
的半径等于椭圆E: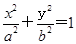 (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为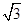 -
-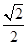 ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).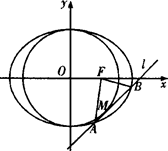
(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:|AF|-|BF|=|BM|-|AM|.
设m为实数,函数f(x)=-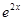 +2x+m,x∈R
+2x+m,x∈R
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当m≤1且x>0时,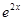 >2
>2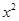 +2mx+1.
+2mx+1.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形;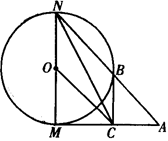
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
已知曲线C1的极坐标方程为ρcos(θ- )=-1,曲线C2的极坐标方程为ρ=2
)=-1,曲线C2的极坐标方程为ρ=2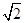 cos(θ-
cos(θ- ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
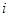 为虚数单位,若复数
为虚数单位,若复数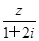 =
=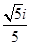 ,则|z|=( )
,则|z|=( )
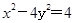 的离心率为( )
的离心率为( )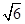
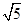
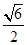

 ·
·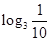 ,V=
,V= ,则输出的S=( )
,则输出的S=( )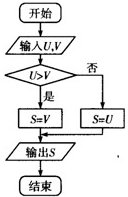

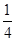




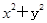 -2x+my-2=0关于抛物线
-2x+my-2=0关于抛物线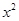 =4y的准线对称,则m=____________.
=4y的准线对称,则m=____________.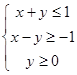 所表示的平面区域为D,若直线
所表示的平面区域为D,若直线 与平面区域D有公共点,则k的取值范围为 .
与平面区域D有公共点,则k的取值范围为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号