广东省东莞市高二下学期期末考试(理科)数学卷
命题“在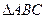 中,若
中,若 是直角,则
是直角,则 一定是锐角.”的证明
一定是锐角.”的证明 过程如下:
过程如下:
假设 不是锐角,则
不是锐角,则 是直角或钝角,即
是直角或钝角,即 ,而
,而 是直角,
是直角,
所以 ,
,
这与三角形的内角和等于 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立,
即 一定是锐角.
一定是锐角.
本题采用的证明方法是
| A.综合法 | B.分析法 | C.反证法 | D.数学归纳法 |
收集一只棉铃虫的产卵数y与温度x的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y与x之间的关系,算出了对应的相关指数R2的值如下表:
| 拟合曲线 |
直 线 |
指数曲线 |
抛物线 |
二次曲线 |
| 回归方程 |
 |
 |
 |
 |
| 相关指数R2 |
0.746 |
0.996 |
0.902 |
0.002 |
则这组数据的回归方程的最佳选择应是
A. |
B. |
C. |
D. |
从4名男生、3名女生中各选出2名组成研究性学习小组,并从选出的4人中再选定1人当组长,则不同选法的种数是
A. |
B. |
C. |
D. |
利用随机变量 来判断“两个分类变量有
来判断“两个分类变量有 关系”的方法称为独立性检验,现通过计算高中生的性别与喜欢数学课程列联表中的数据,得到
关系”的方法称为独立性检验,现通过计算高中生的性别与喜欢数学课程列联表中的数据,得到 ,并且知道
,并且知道 ,那么下列结论中正确的是
,那么下列结论中正确的是
| A.100个高中生中只有5个不喜欢数学 |
| B.100个高中生中只有5个喜欢数学 |
| C.在犯错误的概率不超过0.05的前提下,可以认为高中生的性别与喜欢数学课程有关系 |
| D.在犯错误的概率不超过0.05的前提下,可以认为高中生的性别与喜欢数学课程没有关系 |
如图,矩形的一条对角线与两邻边所成的角分别为 、
、 ,则
,则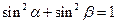 .长方体的一条对角线与三条共顶点的棱所成的角分别为
.长方体的一条对角线与三条共顶点的棱所成的角分别为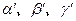 ,与三个共顶点的面所成的角分别为
,与三个共顶点的面所成的角分别为 、
、 、
、 ,用类比推理的方法可知成立的关系式是
,用类比推理的方法可知成立的关系式是
A. |
B. |
C.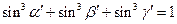 |
D.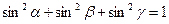 |
从4种不同的颜色中选择若干种给如图所示的4个方格涂色,
每个方格中只涂一种颜色且相邻两格不能涂同一种颜色,则不
同的涂色方法共有
| A.24种 | B.72种 | C.96种 | D.108种 |
 |
某农科所对冬季昼夜温差与某反季节大豆种子发芽多少之间的关系进行分析研究,他们记录了12月1日至5日的昼夜温差与每天100颗种子的发芽数,数据如下表:
| 日 期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差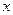 (0C) (0C) |
10 |
11 |
13 |
12 |
8 |
发芽数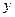 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从五组数据中选取两组,用剩下的3组数据求线性回归方程,再用被选取的两组数据进行检验.
(1) 若先选取的是12月1日和5日的数据,请根据2日至4日的三组数据,求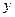 关于
关于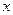 的线性回归方程
的线性回归方程 ;
;
(2) 若由回归方程得到的估计数据与检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试判断(1)中所得的线性回归方程是否可靠?说明理由.
某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列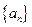 ,且
,且 ,记
,记 .
.
(1)求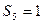 的概率;
的概率;
(2)求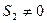 ,
,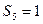 的概率;
的概率;
(3)若记 ,求
,求 .
.
 为纯虚数,其中
为纯虚数,其中 为虚数单位,则实数
为虚数单位,则实数 的值为
的值为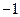





 的分布列为
的分布列为 ……
……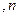 ,且
,且 ,则
,则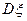 的值为
的值为 
 服从正态分布
服从正态分布 ,且
,且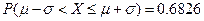 ,则
,则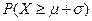 等于
等于 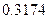

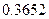
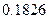
 (
( 为虚数单位)的共轭复数
为虚数单位)的共轭复数 在复平面上对应的点落在第 象限.
在复平面上对应的点落在第 象限.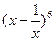 展开式中的常数项等于 .(用数字作答)
展开式中的常数项等于 .(用数字作答)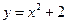 、
、 、
、 所围成
所围成
 在定义域R内可导,
在定义域R内可导,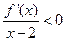 ,且
,且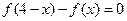 .设
.设 ,
,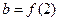 ,
,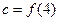 ,则
,则 、
、 、
、 的大小关系为
的大小关系为  .
. .
.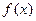 的单调区间;
的单调区间; 上的最大值.(其中
上的最大值.(其中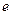 是自然对数的底数)
是自然对数的底数) 对任意实数
对任意实数 都有
都有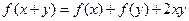 .
.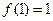 ,求
,求 的值;
的值;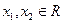 ,求证:
,求证: ;
;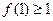 ,求证:
,求证: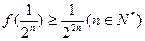 .
.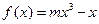 的图象上的点
的图象上的点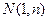 为切点的切线的倾斜角为
为切点的切线的倾斜角为 .
.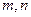 的值;
的值;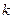 ,使不等式
,使不等式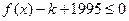 对于
对于 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数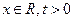 ,比较
,比较 与
与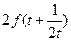 的大小.
的大小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号