[广西]2013届广西桂平市九年级中考二模数学试卷
一粒米的质量约是0.0000217千克,这个质量用科学记数法(保留两个有效数字)表示为( )
| A.2.2×10-5千克 | B.2.2×10-6千克 | C.2.17×10-5千克 | D.2.17×10-6千克 |
一个三角形的两边长分别为3cm和7cm,第三边长为整数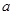 cm,且
cm,且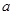 满足
满足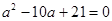 ,则此三角形的周长为( )
,则此三角形的周长为( )
| A.13cm或17cm | B.17cm | C.13cm | D.20cm |
下列命题中,是真命题的是( )
①面积相等的两个直角三角形全等;②对角线互相垂直的四边形是正方形;
③将抛物线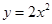 向左平移4个单位,再向上平移1个单位可得到抛物线
向左平移4个单位,再向上平移1个单位可得到抛物线
④两圆的半径R、r分别是方程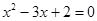 的两根,且圆心距
的两根,且圆心距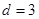 ,则两圆外切.
,则两圆外切.
| A.① | B.② | C.③ | D.④ |
如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD= CD•OA;⑤∠DOC=90°,其中正确的个数共有( )
CD•OA;⑤∠DOC=90°,其中正确的个数共有( )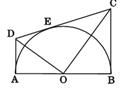
A.1个 B.2个 C.3个 D.4个
如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )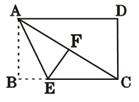
| A.3 | B.4 | C.5 | D.6 |
如图,在 中,
中, ,经过点
,经过点 且与边
且与边 相切的动圆与
相切的动圆与 分别相交于点
分别相交于点 ,则线段
,则线段 长度的最小值是( )
长度的最小值是( )
A. |
B. |
C.4.8 | D.5 |
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2)当直线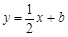 与△ABC有交点时,b的取值范围是( )
与△ABC有交点时,b的取值范围是( )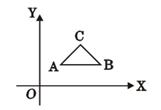
| A.-1≤b≤1 | B.-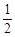 ≤ ≤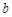 ≤1 ≤1 |
C.-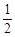 ≤ ≤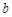 ≤ ≤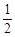 |
D.-1≤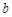 ≤ ≤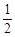 |
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E为DC中点,tan∠C=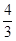 ,则AE的长度为_ __.
,则AE的长度为_ __.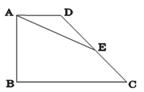
如图, ,过
,过 上到点
上到点 的距离分别为:
的距离分别为: 的点作
的点作 的垂线与
的垂线与 相交,得到并标出一组黑色梯形,它们的面积分别为
相交,得到并标出一组黑色梯形,它们的面积分别为 .观察图中的规律,第n(n为正整数)个黑色梯形的面积
.观察图中的规律,第n(n为正整数)个黑色梯形的面积 .
.
在梯形ABCD中,AB∥CD.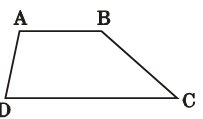
(1)用尺规作图的方法,作∠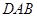 的角平分线AF和梯形的高BG(保留作图痕迹,不写作法和证明);
的角平分线AF和梯形的高BG(保留作图痕迹,不写作法和证明);
(2)若AF 交CD 边交于点E,判断△ADE 的形状(只写结果)
如图,在平面直角坐标系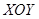 中,一次函数
中,一次函数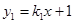 的图象与
的图象与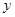 轴交于点A,与x轴交于点B,与反比例函数
轴交于点A,与x轴交于点B,与反比例函数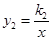 的图象分别交于点
的图象分别交于点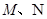 ,已知△AOB的面积为1,点M的纵坐标为2.
,已知△AOB的面积为1,点M的纵坐标为2.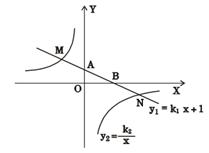
(1)求一次函数与反比例函数的解析式;
(2)直接写出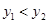 时,
时,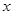 的取值范围.
的取值范围.
“校园手机”现象越来越受到社会的关注,小刘同学随机调查了某一学校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图: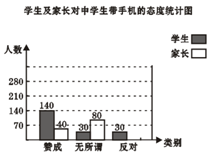

(1)求这次调查的总人数,并补全条形统计图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,小刘决定从初三一班表示赞成的3位家长中随机选择2位进行 深入调查,其中包含小亮和小丁的家长,请你利用画树状图的方法,求出小亮和小丁的家长被同时选中的概率.
如图所示,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.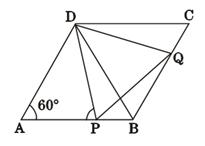
(1)求证:△BDQ≌△ADP;
(2)已知AD=3,AP=2,求cos∠BPQ的值 (结果保留根号)
今年南方某地发生地震,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000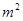 和B种板材24000
和B种板材24000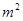 任务.
任务.
⑴如果该厂安排210人生产这两种材,每人每天能生产A种板材60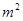 或B种板材
或B种板材
40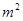 ,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂上述下达任务生产的两种板材搭建甲、乙两种规格的板房
共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
| 板房 |
A种板材(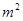 ) ) |
B种板材(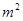 ) ) |
安置人数 |
| 甲型 |
108 |
61 |
12 |
| 乙型 |
156 |
51 |
10 |
问:这400间板房的搭建共有多少种方案?这些方案中能最多地安置灾民的是哪一种?最多能安置灾民多少人?
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.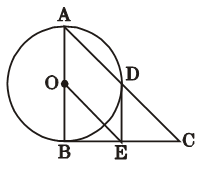
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证: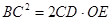
(3)若tanC=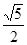 ,DE=2,求AD的长.
,DE=2,求AD的长.




 有意义的
有意义的 的取值范围是( )
的取值范围是( )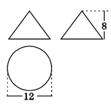


 ,则
,则
 的值为( )
的值为( )


 =
=  的二元一次方程组
的二元一次方程组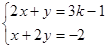 的解满足
的解满足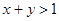 ,则
,则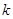 的取值范围是
的取值范围是 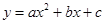 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①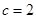 ;②
;②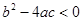 ;③当
;③当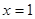 时,
时, 的最小值为
的最小值为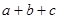 ,④
,④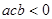 中,正确的有 .
中,正确的有 .
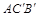 ,则tan
,则tan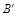 为 .
为 .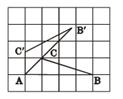
 +
+ –3tan30°+(
–3tan30°+(
 然后从
然后从 的范围内选取一个合适的整数作为
的范围内选取一个合适的整数作为
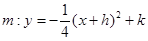 与
与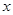 轴的交点为A、B,与
轴的交点为A、B,与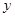 轴的交点为C,顶点为
轴的交点为C,顶点为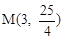 ,将抛物线
,将抛物线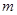 绕点B旋转
绕点B旋转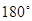 ,得到新的抛物线
,得到新的抛物线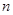 ,它的顶点为D.
,它的顶点为D.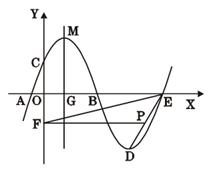
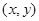 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 粤公网安备 44130202000953号
粤公网安备 44130202000953号